安徽省宿城一中2009届高三第五次模拟
理科数学试卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知集合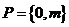 ,
, ,若
,若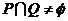 ,则
,则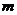 等于( )
等于( )
A.1 B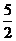 D.1或2
D.1或2
2、设复数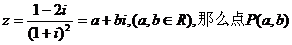 在( )
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知曲线C1: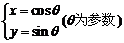 ,曲线C2:
,曲线C2: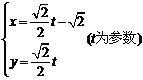 。C1与C2公共点的个数( )
。C1与C2公共点的个数( )
A.1
B
4.已知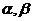 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m//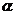 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
A.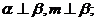 B.
B. C.
C.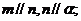 D.
D.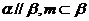
5.已知无穷数列{an}是各项均为正数的等差数列,则有( )
A.< B.≤ C.> D.≥
6.若函数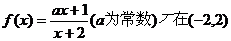 内为增函数,则实数a的取值范围( )
内为增函数,则实数a的取值范围( )
A.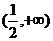 B.
B. C.
C. D.
D.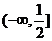
7.设随机变量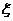 服从正态分布
服从正态分布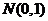 ,若
,若 ,则
,则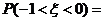 ( )
( )
A.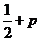 B。
B。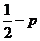 C。
C。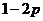 D。
D。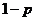
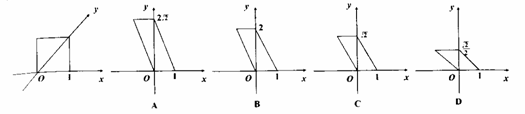
8.用斜二测画法画一个水平放置的平面图形为如下图的一个正方形,则原来图形的形状是( )
9.已知方程 的取值范围( )
的取值范围( )
A.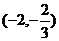 B.
B.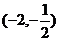 C.
C.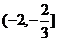 D.
D.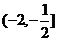
10.按下面图的程序计算,若开始输入的值为x=3,则最后输出的结果是( )

A.6
B.
11、对于某些方程,我们只能由“中间值逼近法”求方程的近似根,如F(x)=2x+x-4,由F(1)<0,F(2)>0,则F(x)=0必有一根在(1,2)内,又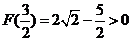 ,则方程必有一根在(1,
,则方程必有一根在(1,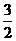 )内,依此类推,现求方程x3+x-1=0的近似根,此方程必有一根在( )内
)内,依此类推,现求方程x3+x-1=0的近似根,此方程必有一根在( )内
A.(0.5,0.6) B。(0.6,0.7) C。(0.7,0.8) D。(0.8,0.9)
12.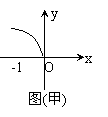 已知偶函数
已知偶函数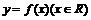 满足
满足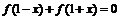 ,又若
,又若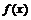 可导,且在
可导,且在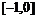 上的导函数图象如图(甲)所示,则
上的导函数图象如图(甲)所示,则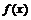 在[2,4]上的大致图象是( )
在[2,4]上的大致图象是( )
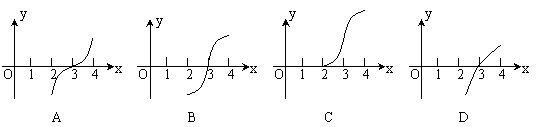
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案填在试题的横线上)
13.若二项式(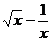 )
)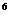 展开式中的第5项是5,则x等于_________
展开式中的第5项是5,则x等于_________
14.点P(3,1)在椭圆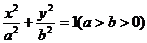
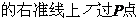
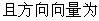 的
的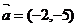 光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
15.关于函数 ,有下列命题
,有下列命题
①其最小正周期为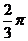 ; ②其图像由
; ②其图像由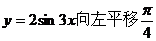 个单位而得到;
个单位而得到;
③其表达式写成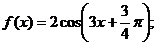 ④在
④在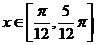 为单调递增函数;
为单调递增函数;
则其中真命题为
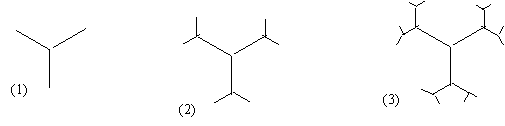
16.图(1)为相互成120°的三条线段,长度均为1,图(2)在第一张图的线段的前端作两条与该线段成120°的线段,长度为其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,则an= .
 |
三、解答题(本大题共6小题,共74分,解答写出必要的文字说明,注明过程及演算步骤)
17.(本小题满分12分)
设函数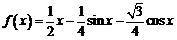 .
.
(1)试判定函数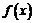 的单调性,并说明理由;
的单调性,并说明理由;
(2)已知函数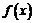 的图象在点
的图象在点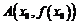 处的切线斜率为
处的切线斜率为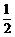 ,求
,求 的值.
的值.
18.(本小题满分12分)
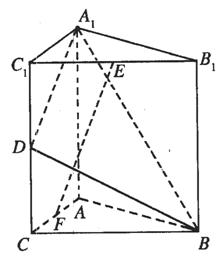
2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队获得每枚金牌的概率均为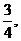 中国乒乓球女队获得每枚金牌的概率均为
中国乒乓球女队获得每枚金牌的概率均为
(I)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
 (II)记中国乒乓球队获得金牌的枚数为ξ,求按此估计ξ的分布列和数学期望Eξ。(结果均用分数表示)
(II)记中国乒乓球队获得金牌的枚数为ξ,求按此估计ξ的分布列和数学期望Eξ。(结果均用分数表示)
19.(本小题满分12分)如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求二面角B―A1D―A的大小;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD? 若存在,确定其位置并证明结论;若不存在,说明理由.
20.(本小题满分12分)
已知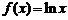 ,
,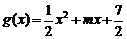 (
(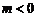 ),直线
),直线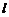 与函数
与函数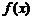 、
、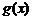 的图像都
的图像都
相切,且与函数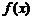 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线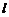 的方程及
的方程及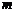 的值;
的值;
(Ⅱ)若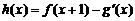 (其中
(其中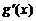 是
是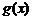 的导函数),求函数
的导函数),求函数 的最大值;
的最大值;
(Ⅲ)当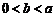 时,求证:
时,求证: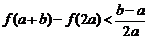 .
.
21.设F1、F2分别是椭圆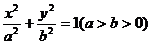 的左、右焦点,B是其上顶点,椭圆的右准线与x轴交于点N,已知
的左、右焦点,B是其上顶点,椭圆的右准线与x轴交于点N,已知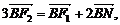 且
且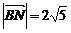 .
.
(Ⅰ)求此椭圆的方程;
(Ⅱ)若M是坐标平面内一动点,G是三角形MF1F2的重心,且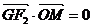 ,其中O是坐标原点,求动点M的轨迹C的方程;
,其中O是坐标原点,求动点M的轨迹C的方程;
(Ⅲ)点P是此椭圆上一点,但非短轴端点,并且过P可作(Ⅱ)中所求得轨迹C的两条不同的切线,Q、R是两个切点,求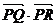 的最小值.
的最小值.
22.(本小题满分14分)
已知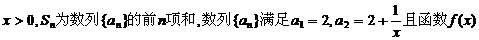
对于任意的
(I)求函数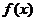 的解析式;
的解析式;
(II)求数列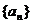 的通项公式;
的通项公式;
(III)若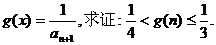
答案
一 选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
A
D
B
A
B
A
A
D
B
B
二 填空题:
13.3
14.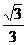 15.
①③④ 16. 3n
15.
①③④ 16. 3n
三、解答题
17.解:(1)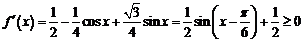 ,
,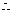
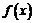 定义域内单调递增.
定义域内单调递增.
(2)由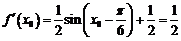 ,得:
,得: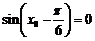 .
.
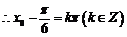 ,得
,得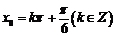 ,
,
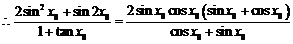
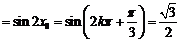 .
.
18.解:(I)设中国乒乓球男队获0枚金牌,女队获1枚金牌为事件A,中国乒乓球男队获1枚金牌,女队获2枚金牌为事件B,那么,
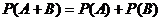
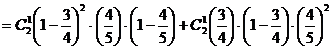
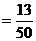
(II)根据题意中国乒乓球队获得金牌数是一随机变量ξ,
它的所有可能取值为0,1,2,3,4(单位:枚)。那么,
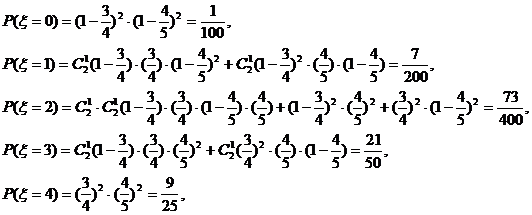 则概率分布为:
则概率分布为:
ξ
0
1
2
3
4
P
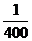

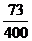
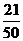
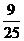
………………10分
那么,所获金牌数的数学期望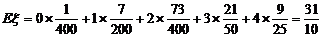 (枚)
(枚)
答:中国乒乓球队获得金牌数的期望为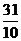 枚。
枚。
19.解法一:(1)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM
∵BC⊥平面ACC1A1 ∴CM为BM在平面A1C1CA的内射影
∴BM⊥A1G ∴∠CMB为二面角B―A1D―A的平面角
平面A1C1CA中,C1C=CA=2,D为C1C的中点
∴CG=2,DC=1 在直角三角形CDG中,
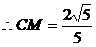
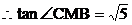 ,
,
即二面角B―A1D―A的大小为
(2)在线段AC上存在一点F,使得EF⊥平面A1BD其位置为AC中点,证明如下:
∵A1B1C1―ABC为直三棱柱 , ∴B1C1//BC
∵由(1)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA
∵EF在平面A1C1CA内的射影为C1F ,F为AC中点 ∴C1F⊥A1D ∴EF⊥A1D同理可证EF⊥BD, ∴EF⊥平面A1BD
∵E为定点,平面A1BD为定平面,点F唯
解法二:(1)∵A1B1C1―ABC为直三棱住 C1C=CB=CA=2 , AC⊥CB D、E分别为C1C、B1C1的中点, 建立如图所示的坐标系得
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2)
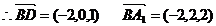 设平面A1BD的法向量为
设平面A1BD的法向量为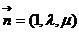
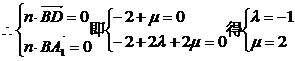
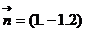
平面ACC1A1的法向量为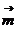 =(1,0,0)
=(1,0,0) 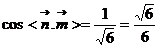
即二面角B―A1D―A的大小为
(2)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD
欲使EF⊥平面A1BD 由(2)知,当且仅当 //
//
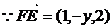
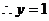
∴存在唯一一点F(0,1,0)满足条件. 即点F为AC中点
20解:(Ⅰ)依题意知:直线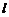 是函数
是函数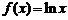 在点
在点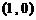 处的切线,故其斜率
处的切线,故其斜率
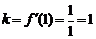 ,
,
所以直线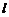 的方程为
的方程为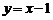 .
.
又因为直线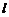 与
与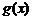 的图像相切,所以由
的图像相切,所以由
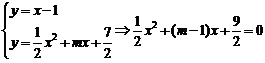 ,
,
得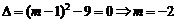 (
(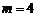 不合题意,舍去);
不合题意,舍去);
(Ⅱ)因为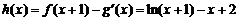 (
(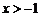 ),所以
),所以
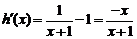 .
.
当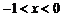 时,
时,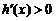 ;当
;当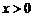 时,
时,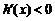 .
.
因此, 在
在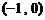 上单调递增,在
上单调递增,在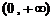 上单调递减.
上单调递减.
因此,当 时,
时, 取得最大值
取得最大值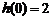 ;
;
(Ⅲ)当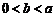 时,
时,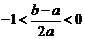 .由(Ⅱ)知:当
.由(Ⅱ)知:当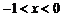 时,
时,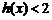 ,即
,即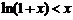 .因此,有
.因此,有
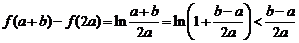
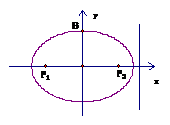 21.(Ⅰ)设
21.(Ⅰ)设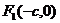 ,
,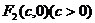 ,
,
则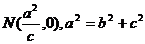 ,
,
因为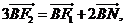
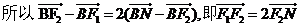 ,
,
所以(2c,0)=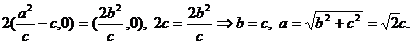
从而N(2c,0),B(0,c)
所以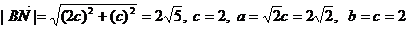
因此所求椭圆的方程为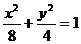 .
.
(Ⅱ)设M(x,y),则由(1)得F1(-2,0),F2(2,0),
所以G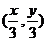 ,从而
,从而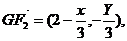
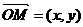 .因为
.因为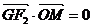
所以有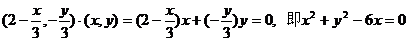
由于G是三角形MF1F2的重心,即M,F1,F2应当是一个三角形的三个顶点,
因此所求的轨迹C的方程为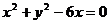 (y≠0).
(y≠0).
(Ⅲ)由(Ⅱ)知轨迹C的方程为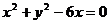 ,即
,即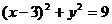 (y≠0).
(y≠0).
显然轨迹C是以点C(3,0)为圆心,半径r=3的圆除去两点(0,0)和(6,0)剩余部分的部分曲线.
设P(m,n),则根据平面几何知识得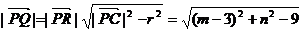
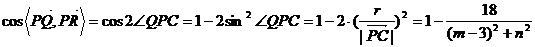 从而根据平面向量数量积的定义及均值不等式得
从而根据平面向量数量积的定义及均值不等式得
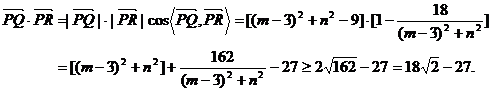
当且仅当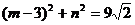 时,取“=” (※)
时,取“=” (※)
由点P(m,n)在椭圆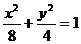 上(非短轴端点),并且在圆
上(非短轴端点),并且在圆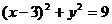 外,可知
外,可知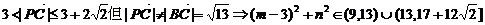
由于 ,所以条件(※)的要求满足.
,所以条件(※)的要求满足.
因此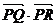 的最小值为
的最小值为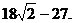
22.(本小题满分14分)
解:(I)把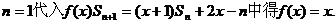 、
、
(II)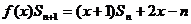 , ①
, ①
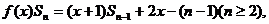 ②
②
①式减②式得,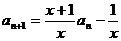 ,
,
变形得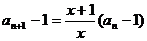 ,
,
又因为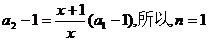 时上式也成立。
时上式也成立。
所以,数列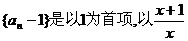 为公比的等比数列,
为公比的等比数列,
所以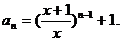
(III)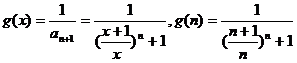 ,
,
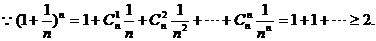
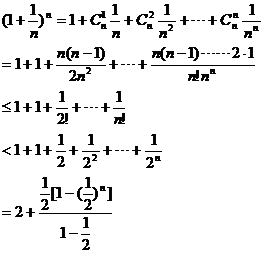
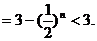 所以
所以