摘要:17.解:(1).定义域内单调递增.
网址:http://m.1010jiajiao.com/timu_id_160932[举报]
设f(x)是定义在(0,+∞)上的单调递增函数,且对于定义域内的任意x,y有![]() 成立.
成立.
(1)求f(1).
(2)证明:对于定义域内的任意x,y,有f(xy)=f(x)+f(y)成立.
(3)设f(3)=1,解关于x的不等式f(x)≥2+f(![]() ),其中P
),其中P![]() R
R
已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)定义域内单调递增;
(2)记g(x)=log 2(2x-1).若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
查看习题详情和答案>>
(1)求证:函数f(x)定义域内单调递增;
(2)记g(x)=log 2(2x-1).若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
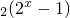 .若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
.若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.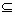 D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.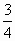 x+
x+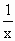 (x∈R+)是否为闭函数?并说明理由;
(x∈R+)是否为闭函数?并说明理由;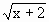 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.