网址:http://m.1010jiajiao.com/timu_id_160976[举报]
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点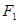 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看习题详情和答案>>
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r= =
= ,
,
故所求圆的方程为: +
+ =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r= =
= ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: +
+ =
=
 , ………………………6分
, ………………………6分
解得a=1,b=-2,  =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
其它方法相应给分
查看习题详情和答案>>
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l过P(-
| 1 |
| 2 |
| 1 |
| 2 |
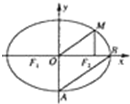 如图所示,F1、F2分别是椭圆
如图所示,F1、F2分别是椭圆 已知矩形ABCD的边AB=4cm,BC=3cm,如图所示,矩形的顶点A,B为某一椭圆的两个焦点,且椭圆经过矩形的另外两个顶点C,D,试建立适当的坐标系,求椭圆的方程.
已知矩形ABCD的边AB=4cm,BC=3cm,如图所示,矩形的顶点A,B为某一椭圆的两个焦点,且椭圆经过矩形的另外两个顶点C,D,试建立适当的坐标系,求椭圆的方程.