第二十五讲 选 择 题 的 解 法
一、题型特点:
1.高考数学试题中,选择题注重多个知识点的小型综合,渗透各种数学思想和方法,体现以考查“三基”为重点的导向,能否在选择题上获取高分,对高考数学成绩影响重大.解答选择题的基本要求是四个字――准确、迅速.
2.选择题主要考查基础知识的理解、基本技能的熟练、基本计算的准确、基本方法的运用、考虑问题的严谨、解题速度的快捷等方面. 解答选择题的基本策略是:要充分利用题设和选择支两方面提供的信息作出判断。一般说来,能定性判断的,就不再使用复杂的定量计算;能使用特殊值判断的,就不必采用常规解法;能使用间接法解的,就不必采用直接解;对于明显可以否定的选择应及早排除,以缩小选择的范围;对于具有多种解题思路的,宜选最简解法等。解题时应仔细审题、深入分析、正确推演、谨防疏漏;初选后认真检验,确保准确。
3.解数学选择题的常用方法,主要分直接法和间接法两大类.直接法是解答选择题最基本、最常用的方法;但高考的题量较大,如果所有选择题都用直接法解答,不但时间不允许,甚至有些题目根本无法解答.因此,我们还要掌握一些特殊的解答选择题的方法.
二、例题解析
1.直接求解法 涉及数学定义、定理、法则、公式的应用的问题,常通过直接演算得出结果,与选择支进行比照,作出选择,称之直接求解法.
例1、 圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为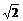 的点共有( )
的点共有( )
A.1个 B.2个 C.3个 D.4个
解 :本题的关键是确定已知直线与圆的相对位置,这就需对圆心到直线的距离作定量分析.将圆的方程化为(x+1)2+(y+2)2=(2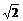 )2,∴ r=2
)2,∴ r=2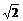 .∵ 圆心(-1,-2)到直线x+y+1=0的距离d=
.∵ 圆心(-1,-2)到直线x+y+1=0的距离d=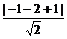 =
=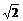 ,恰为半径的一半.故选C.
,恰为半径的一半.故选C.
例2、设F1、F2为双曲线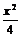 -y2=1的两个焦点,点P在双曲线上满足∠F1PF2=90o,则△F1PF2的面积是( )
-y2=1的两个焦点,点P在双曲线上满足∠F1PF2=90o,则△F1PF2的面积是( )
A.1
B.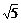 /2
C.2
D.
/2
C.2
D.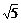
解 ∵ |PF1|-|PF2|=±2a=±4,∴ |PF1|2+|PF2|2-2|PF1|?|PF2|=16,
∵ ∠F1PF2=90o,∴ 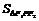 =
=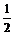 |PF1|?|PF2|=
|PF1|?|PF2|=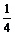 (|PF1|2+|PF2|2-16).
(|PF1|2+|PF2|2-16).
又∵ |PF1|2+|PF2|2=(2c)2=20.∴
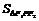 =1,选A.
=1,选A.
例3、
椭圆mx2+ny2=1与直线x+y=1交于A、B两点,过AB中点M与原点的直线斜率为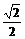 ,则
,则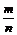 的值为( )
的值为( )
A.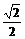 B.
B.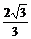 C.1
D.
C.1
D.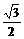
分析:命题:“若斜率为k(k≠0)的直线与椭圆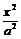 +
+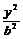 =1(或双曲线
=1(或双曲线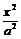 -
-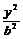 =1)相交于A、B的中点,则k?kOM=-
=1)相交于A、B的中点,则k?kOM=-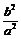 (或k?kOM=
(或k?kOM=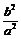 ),”(证明留给读者)在处理有关圆锥曲线的中点弦问题中有着广泛的应用.运用这一结论,不难得到:
),”(证明留给读者)在处理有关圆锥曲线的中点弦问题中有着广泛的应用.运用这一结论,不难得到:
解 ∵ kAB?kOM=-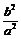 =-
=-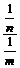 =-
=-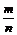 ,∴
,∴ 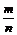 =-kAB?kOM=1?
=-kAB?kOM=1?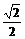 =
=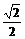 ,故选A.
,故选A.
2.直接判断法
涉及有关数学概念的判断题,需依据对概念的全面、正确、深刻的理解而作出判断和选择.
例1、甲:“一个二面角的两个半平面分别垂直于另一个二面角的两个半平面”,乙:“两个二面角相等或互补.”则甲是乙的( )
A.充分而非必要条件 B.必要而非充分条件
C.充要条件 D.既非充分又非要条件
分析 显然“乙Þ甲”不成立,因而本题关键是判断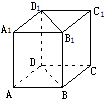
“甲Þ乙”是否成立?由反例:正方体中,二面角A1-AB
-C与B1-DD1-A满足条件甲(图31-1),但它们的度数
分别为90o和45o,并不满足乙,故应选D.
例2、下列四个函数中,既不是奇函数,也不是偶函数的是( )
A.f(x)=x+lg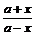 B.f(x)=(x-1)
B.f(x)=(x-1)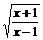
C.f(x)=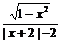 D.f(x)=
D.f(x)=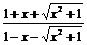
解 由于选择支B给出的函数的定义域为[-1,1],该定义区间关于原点不对称,故选B.
3、特殊化法(即特例判断法)
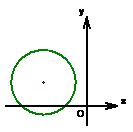 例1.如右下图,定圆半径为a,圆心为 ( b ,c ), 则直线ax+by+c=0
例1.如右下图,定圆半径为a,圆心为 ( b ,c ), 则直线ax+by+c=0
与直线 x?y+1=0的交点在( B )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
提示:取满足题设的特殊值a=2,b=?3,c=1
解方程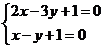 得
得 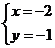 于是排除A、C、D,故应选B
于是排除A、C、D,故应选B
例2.函数f(x)=Msin(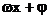 ) (
) (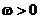 )在区间[a,b]上是增函数,且f(a)=?M,
)在区间[a,b]上是增函数,且f(a)=?M,
f(b)=M,则函数g(x)=Mcos(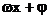 )在[a,b]上( C
)
)在[a,b]上( C
)
A.是增函数 B.是减函数 C.可以取得最大值M D.可以取得最小值?M
解:取特殊值。令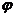 =0,
=0,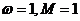 ,则
,则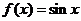
因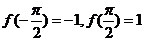 ,则
,则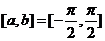 ,这时
,这时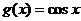 ,
显然应选C
,
显然应选C
例3.已知等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为( C )
A.130 B.170 C.210 D.260
解:特殊化法。令m=1,则a1=S1=30,又a1+a2=S2=100 ∴a2=70, ∴等差数列的公差d=a2?a1=40,于是a3=a2+d=110, 故应选C
例4.已知实数a,b均不为零,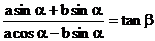 ,且
,且 ,则
,则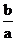 等于( B )
等于( B )
A.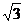 B.
B.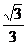 C.?
C.?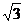 D.?
D.?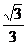
提示:特殊化法。取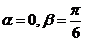 ,则
,则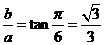 故应选B
故应选B
4、排除法(筛选法)
例1.设函数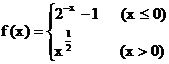 ,若f(x0)>1,则x0的取值范围是( D )
,若f(x0)>1,则x0的取值范围是( D )
A.(?1,1) B.(?1,+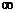 ) C.(?
) C.(?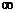 ,?2)
,?2)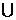 (0,+
(0,+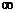 ) D.(?
) D.(?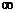 ,?1)
,?1)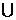 (1,+
(1,+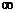 )
)
例2.已知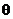 是第三象限角,|cos
是第三象限角,|cos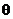 |=m,且
|=m,且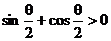 ,则
,则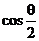 等于( D )
等于( D )
A.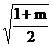 B.?
B.?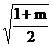 C.
C. D.?
D.?
例3.已知二次函数f(x)=x2+2(p?2)x+p,若f(x)在区间[0,1]内至少存在一个实数c,使f( c)>0,
则实数p的取值范围是( C )
A.(1,4)
B.(1,+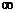 ) C.(0,+
) C.(0,+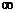 ) D.(0,1)
) D.(0,1)
点评:排除法,是从选择支入手,根据题设条件与各选择支的关系,逐个淘汰与题设矛盾的选择支,从而筛选出正确答案。
5、数形结合法(图象法) 根据题目特点,画出图象,得出结论。
例1.对于任意x∈R,函数f(x)表示?x+3,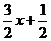 ,x2?4x+3中的较大者,则f(x)的最小值是( A )
,x2?4x+3中的较大者,则f(x)的最小值是( A )
A.2 B.3 C.8 D.?1
例2.已知向量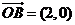 ,向量
,向量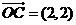 ,向量
,向量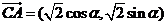 ,则向量
,则向量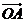 与向量
与向量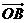 的夹角的取值范围是( D )
的夹角的取值范围是( D )
A.[0,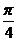 ]
B.[
]
B.[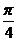 ,
,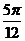 ] C.[
] C.[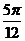 ,
,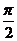 ] D.[
] D.[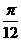 ,
,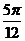 ]
]
例3.已知方程|x?2n|=k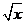 (n∈N*)在区间[2n?1,2n+1]上有两个不相等的实数根,则k的取值范围是( B )
(n∈N*)在区间[2n?1,2n+1]上有两个不相等的实数根,则k的取值范围是( B )
A.k>0 B.0<k≤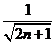 C.
C.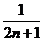 ≤k≤
≤k≤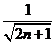 D.以上都不是
D.以上都不是
6、代入检验法(验证法)
将选择支中给出的答案(尤其关注分界点),代入题干逐一检验,从而确定正确答案的方法为验证法。
例1.已知a,b是任意实数,记|a+b|,|a?b|,|b?1|中的最大值为M,则(D )
A.M≥0 B.0≤M≤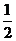 C.M≥1 D.M≥
C.M≥1 D.M≥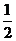
解:把M=0代入,排除A、B;再把M=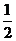 代入检验满足条件,排除C。
代入检验满足条件,排除C。
例2.已知二次函数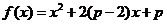 ,若在区间[0,1]内至少存在一个实数c,使
,若在区间[0,1]内至少存在一个实数c,使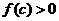 ,则实数p的取值范围是( C )
,则实数p的取值范围是( C )
A.(1,4) B.(1,+∞) C.(0,+∞) D.(0,1)
解:取p=1代入检验。
例3.(2004广东)变量x,y满足下列条件: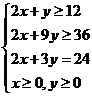
则使得z=3x+2y的值的最小的(x,y)是( B )
A.(4.5,3) B.(3,6) C.(9,2) D.(6,4)
解:一一代入检验。代入运算后比较大小。
7、推理分析法
通过对四个选择支之间的逻辑关系的分析,达到否定谬误支,肯定正确支的方法,称之为逻辑分析法,例如:若“(A)真 Þ (B)真”,则(A)必假,否则将与“只有一个选择支正确”的前提相矛盾.
例1 当xÎ[-4,0]时,a+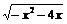 ≤
≤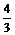 x+1恒成立,则a的一个可能值是( )
x+1恒成立,则a的一个可能值是( )
A.5
B.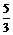 C.-
C.-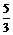 D.-5
D.-5
解 ∵ 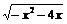 ≥0, ∴ (A)真Þ(B)真Þ(C)真Þ(D)真,
∴ (D)真.
≥0, ∴ (A)真Þ(B)真Þ(C)真Þ(D)真,
∴ (D)真.
例3、已知sinq =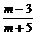 ,cosq =
,cosq =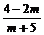 (
(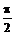 <q <p),则tg
<q <p),则tg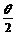 =( ).
=( ).
A.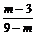 B.|
B.|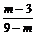 |
C.
|
C.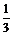 D.5
D.5
解 因受条件sin2q +cos2q =1的制约,故m为一确定值,于是sinq 、cosq 的值应与m无关,进而推知tg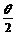 的值与m无关,∵
的值与m无关,∵ 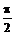 <q <p, ∴
<q <p, ∴ 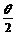 Î(
Î(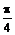 ,
,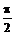 ),∴
tg
),∴
tg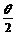 >1,故选(D).
>1,故选(D).
注:直接运用半角公式求tg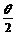 ,将会错选(A).若直接计算,由(
,将会错选(A).若直接计算,由(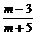 )2+(
)2+(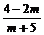 )2=1,可得m=0或m=8,∵
)2=1,可得m=0或m=8,∵ 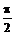 <q <p, ∴ sinq >0,cosq <0,故应舍去m=0,取m=8,得sinq =
<q <p, ∴ sinq >0,cosq <0,故应舍去m=0,取m=8,得sinq =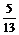 ,cosq =
,cosq =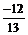 ,再由半角公式求出tg=
,再由半角公式求出tg=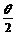 =5,也不如上述解法简捷.
=5,也不如上述解法简捷.
三、练习
1已知点P(sinα-cosα,tanα)在第一象限,则在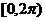 内α的取值范围为( B )
内α的取值范围为( B )
A 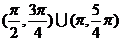 B
B 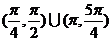
C 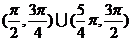 D
D 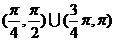
2一个直角三角形的三内角成等比数列,则其最小内角为( B )
A 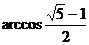 B
B 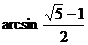 C
C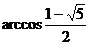 D
D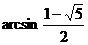
3若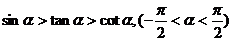 ,则
,则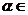 ( B )
( B )
A 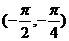 B
B 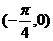 C
C 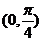 D
D 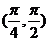
4函数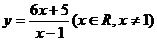 的反函数为( B )
的反函数为( B )
A 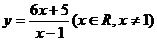 B
B 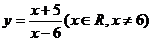
C 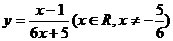 D
D 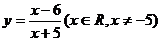
5已知函数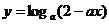 在[0,1]上是x的减函数,则a的取值范围为( B )
在[0,1]上是x的减函数,则a的取值范围为( B )
A (0,1) B (1,2) C (0,2) D 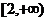
6.(07天津)设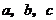 均为正数,且
均为正数,且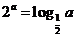 ,
,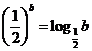 ,
,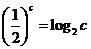 .则( A )
.则( A )
A.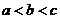 B.
B.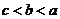 C.
C.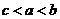 D.
D.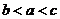
7设f(x)是定义在实数集R上的任意一个增函数,且F(x)=f(x)-f(-x),那么F(x)应为( A )
A 增函数且是奇函数 B增函数且是偶函数
C 减函数且是奇函数 D减函数且是偶函数
解: 取f(x)=x,知F(x)=x-(-x)=2x,故选A。
8定义在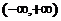 上的奇函数
上的奇函数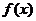 为增函数,偶函数
为增函数,偶函数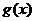 在区间
在区间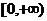 的图象与
的图象与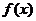 的图象重合,设
的图象重合,设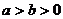 ,给出下列不等式:
,给出下列不等式:
1)f(b)-f(-a)>g(a)-g(-b) 2) f(b)-f(-a)<g(a)-g(-b)
3) f(a)-f(-b)>g(b)-g(-a) 4) f(a)-f(-b)<g(b)-g(-a)
其中成立的是( C )
A 1)与2) B 2)与3) C 1)与3) D 2)与4)
9若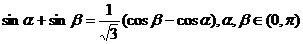 ,则
,则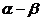 的值为( D )
的值为( D )
A 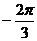 B
B 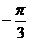 C
C 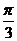 D
D 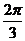
10将直线3x-y+2=0绕原点按逆时针方向旋转900,得到的直线方程为( A )
A x+3y+2=0 B x+3y-2=0 C x-3y+2=0 D x-3y-2=0
11已知集合A=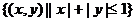 ,B=
,B=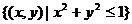 ,C
,C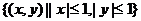 的则A、B、C的关系是( C ).
的则A、B、C的关系是( C ).
A.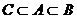 B.
B. 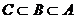
C.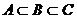 D.
D. 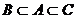
12集合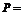 {
{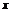 ,1},
,1},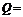 {
{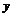 ,1,2},其中
,1,2},其中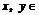 {1,2,…,9}且
{1,2,…,9}且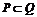 ,把满足上述条件的一对有序整数(
,把满足上述条件的一对有序整数(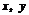 )作为一个点,这样的点的个数是(B)
)作为一个点,这样的点的个数是(B)
(A)9 (B)14 (C)15 (D)21
13已知函数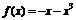 ,
,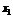 ,
,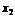 ,
,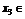 R,且
R,且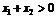 ,
,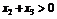 ,
,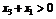 ,则
,则
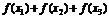 的值(B)
的值(B)
(A)一定大于零 (B)一定小于零 (C)等于零 (D)正负都有可能
14已知1是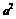 与
与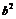 的等比中项,又是
的等比中项,又是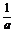 与
与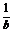 的等差中项,则
的等差中项,则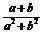 的值是 (D)
的值是 (D)
(A)1或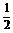 (B)1或
(B)1或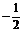 (C)1或
(C)1或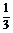 (D)1或
(D)1或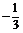
15平面直角坐标系中,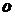 为坐标原点,已知两点
为坐标原点,已知两点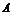 (2,-1),
(2,-1),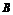 (-1,3),若点
(-1,3),若点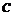 满足
满足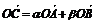 其中0≤
其中0≤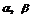 ≤1,且
≤1,且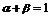 ,则点
,则点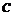 的轨迹方程为(C)
的轨迹方程为(C)
(A)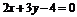 (B)
(B)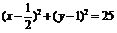
(C)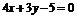 (-1≤
(-1≤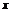 ≤2)
(D)
≤2)
(D)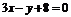 (-1≤
(-1≤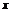 ≤2)
≤2)
16.已知定义域为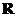 的函数
的函数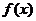 在
在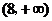 上为减函数,且函数
上为减函数,且函数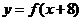 为偶函数,则( D )
为偶函数,则( D )
A.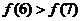 B.
B.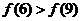 C.
C.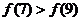 D.
D.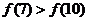
17下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是(D)
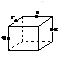
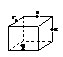
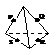
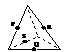
(A) (B) (C) (D)
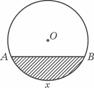
18如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB
所围成的弓形面积的2倍,则函数y=f(x)的图象是 ( D )
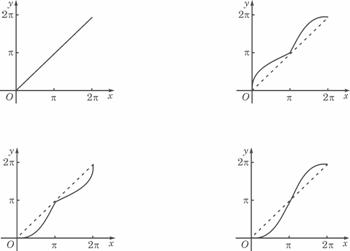
19为确保信息安全,信息需加密传输,发送方由明文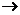 密文(加密),接收方由密文
密文(加密),接收方由密文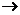 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文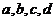 对应密文
对应密文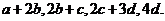 例如,明文
例如,明文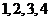 对应密文
对应密文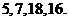 当接收方收到密文
当接收方收到密文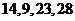 时,则解密得到的明文为(B)
时,则解密得到的明文为(B)
(A)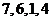 (B)
(B)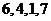 (C)
(C)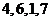 (D)
(D)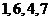
20关于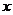 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是 (A)
A. 0
B.
21设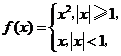
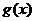 是二次函数,若
是二次函数,若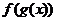 的值域是
的值域是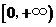 ,则
,则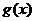 的值域是( C )
的值域是( C )
A.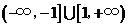 B.
B.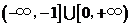
C.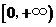 D.
D.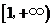
22如果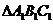 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于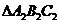 的三个内角的正弦值,则( D )
的三个内角的正弦值,则( D )
A.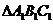 和
和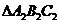 都是锐角三角形
都是锐角三角形
B.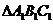 和
和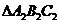 都是钝角三角形
都是钝角三角形
C.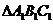 是钝角三角形,
是钝角三角形,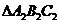 是锐角三角形
是锐角三角形
D.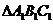 是锐角三角形,
是锐角三角形,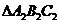 是钝角三角形
是钝角三角形
23已知非零向量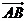 与
与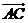 满足
满足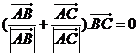 且
且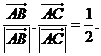 则
则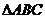 为(A)
为(A)
(A)等边三角形 (B)直角三角形
(C)等腰非等边三角形 (D)三边均不相等的三角形
24已知双曲线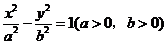 的左、右焦点分别为
的左、右焦点分别为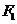 ,
,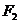 ,
,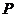 是准线上一点,且
是准线上一点,且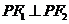 ,
,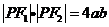 ,则双曲线的离心率是( B )
,则双曲线的离心率是( B )
A.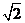 B.
B.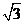 C.
C.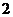 D.
D.
 25如图,平面中两条直线
25如图,平面中两条直线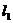 和
和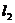 相交于点O,对于平面上任意一点M,若
相交于点O,对于平面上任意一点M,若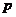 、
、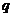 分别是M到直线
分别是M到直线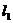 和
和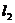 的距离,则称有序非负实数对(
的距离,则称有序非负实数对(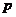 ,
,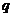 )是点M的“距离坐标”.已知常数
)是点M的“距离坐标”.已知常数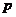 ≥0,
≥0,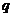 ≥0,给出下列命题:
≥0,给出下列命题:
①若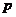 =
=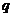 =0,则“距离坐标”为(0,0)的点
=0,则“距离坐标”为(0,0)的点
有且仅有1个;
②若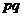 =0,且
=0,且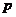 +
+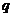 ≠0,则“距离坐标”为
≠0,则“距离坐标”为
(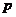 ,
,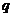 )的点有且仅有2个;
)的点有且仅有2个;
③若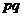 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(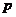 ,
,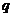 )的点有且仅有4个.
)的点有且仅有4个.
上述命题中,正确命题的个数是( D )
(A)0; (B)1; (C)2; (D)3.
26(06江西)对于R上可导的任意函数f(x),若满足(x-1)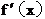 ³0,则必有( C )
³0,则必有( C )
A.
f(0)+f(2)<
C. f(0)+f(2)³