第二讲 函数图象
★★★高考在考什么
 【考题回放】
【考题回放】
1.图中的图象所表示的函数的解析式为( )
A.

B.

C.

D.

2.客车从甲地以 与时间
与时间 之间关系的图象中,正确的是( C )
之间关系的图象中,正确的是( C )
 |
3.函数 的图象和函数
的图象和函数 的图象的交点个数是( B )
的图象的交点个数是( B )
A.4 B.
4.若函数 的图象按向量
的图象按向量 平移后,得到函数
平移后,得到函数 的图象,则向量
的图象,则向量 ( A )
( A )
A. B.
B. C.
C. D.
D.
5.若函数 的反函数为
的反函数为 ,则函数
,则函数 与
与 的图象可能是( A )
的图象可能是( A )


A. B. C. D.
6.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 (毫克)与时间
(毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 与
与 的函数关系式为
的函数关系式为 (
( 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题:
(I)从药物释放开始,每立方米空气中的含药量 (毫克)与时间
(毫克)与时间 (小时)之间的函数关系式为 ;
(小时)之间的函数关系式为 ;
 (II)据测定,当空气中每立方米的含药量降低到
(II)据测定,当空气中每立方米的含药量降低到 毫克以下时,学生方可进教室,那么药物释放开始,至少需要经过 小时后,学生才能回到教室.
毫克以下时,学生方可进教室,那么药物释放开始,至少需要经过 小时后,学生才能回到教室.
6. ;0.6
;0.6
★★★高考要考什么
一、奇函数( 的图象关于原点对称;偶函数(
的图象关于原点对称;偶函数( 图象关于
图象关于 轴对称。
轴对称。
引申:若 ,则
,则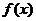 的图象关于点(1,0)对称;
的图象关于点(1,0)对称;
若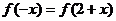 ,则
,则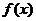 的图象关于直线
的图象关于直线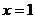 对称;
对称;
若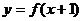 是奇函数,则
是奇函数,则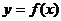 关于点(1,0)对称;
关于点(1,0)对称;
若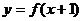 是偶函数,则
是偶函数,则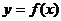 关于直线
关于直线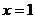 对称;
对称;
区别: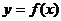 与
与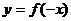 的图象关于
的图象关于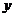 轴对称;
轴对称;
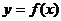 与
与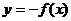 的图象关于
的图象关于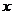 轴对称;
轴对称;
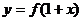 与
与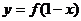 的图象关于
的图象关于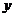 轴对称;
轴对称;
二、翻折变换:
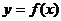 和
和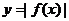 图象间的关系____ ;
图象间的关系____ ;
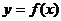 和
和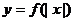 图象间的关系_____ ;
图象间的关系_____ ;
如:作出: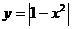 与
与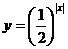 的图象
的图象
★★★ 突 破 重 难 点
【范例1】 定义域和值域均为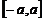 (常数
(常数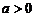 )的函数
)的函数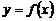 和
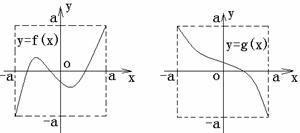
和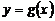 的图像如图所示,给出下列四个命题:
的图像如图所示,给出下列四个命题:
(1)方程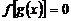 有且仅有三个解;
有且仅有三个解;
 (2)方程
(2)方程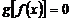 有且仅有三个解;
有且仅有三个解;
(3)方程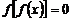 有且仅有九个解;
有且仅有九个解;
(4)方程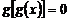 有且仅有一个解。
有且仅有一个解。
那么,其中正确命题的个数是 (1)、(4) 。
变式:函数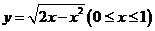 的图象与它的反函数图象所围成的面积是
的图象与它的反函数图象所围成的面积是
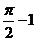
【范例2】 设曲线C的方程是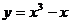 ,将C沿
,将C沿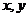 轴正向分别平移
轴正向分别平移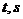 单位长度后得曲线
单位长度后得曲线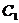 ;(1)写出曲线
;(1)写出曲线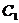 的方程;(2)证明曲线
的方程;(2)证明曲线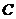 与曲线
与曲线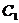 关于点
关于点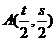 对称;(3)如果曲线
对称;(3)如果曲线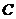 与曲线
与曲线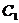 有且仅有一个公共点,证明
有且仅有一个公共点,证明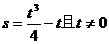 。
。
解:(1)曲线C1的方程为 y=(x-t)3 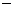 (x-t)+s
(x-t)+s
(2)证明:在曲线C上任取一点B1(x1,y1)。。设B2(x2,y2)是B1关于点A的对称点,则有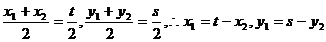
代入曲线C的方程,得x2和y2满足方程:
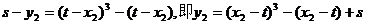
可知点B2(x2,y2)在曲线C1上。
反过来,同样可以证明,在曲线C1上的 点关于点A的对称点在曲线C上。因此,曲线C与C1关于点A对称。
(Ⅲ)证明:因为曲线C与C1有且仅有一个公共点,所以,方程组
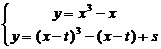
有且仅有一组解。消去y,整理得 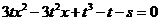
这个关于x的一元二次方程有且仅有一个根。所以t≠0并且其根的判别式
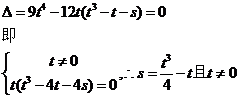
变式:已知函数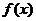 的图象与函数
的图象与函数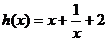 的图象关于点A(0,1)对称.(1)求
的图象关于点A(0,1)对称.(1)求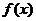 的解析式;(2)若
的解析式;(2)若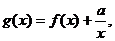 且
且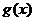 在
在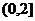 上为减函数,求实数
上为减函数,求实数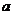 的取值范围.
的取值范围.
解:(1)设点M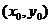 是函数
是函数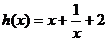 任意点,点M关于A(0,1)的对称点为P
任意点,点M关于A(0,1)的对称点为P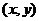 ,
,
则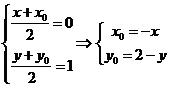 ,代入
,代入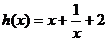 得:
得: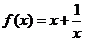 。
。
(2)设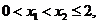 则
则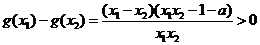 恒成立,
恒成立,
 恒成立,
恒成立,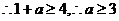
【范例3】已知f(x)是二次函数,不等式f(x)<0的解集是(0,5)且f(x)在区间[-1,4]上的最大值是12。
(I)求f(x)的解析式;
(II)是否存在实数m使得方程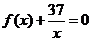 在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出m的取值范围;若不存在,说明理由。
在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出m的取值范围;若不存在,说明理由。
解:(I)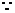
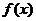 是二次函数,且
是二次函数,且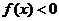 的解集是
的解集是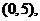
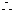 可设
可设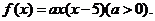
\ f(x)在区间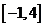 上的最大值是
上的最大值是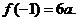
由已知,得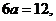
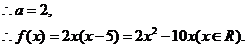
(II)方程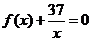 等价于方程
等价于方程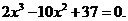
设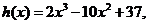 则
则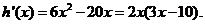
当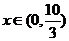 时,
时,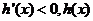 是减函数;
是减函数;
当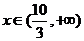 时,
时,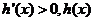 是增函数。
是增函数。
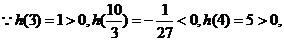
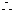 方程
方程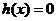 在区间
在区间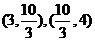 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间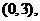
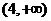 内没有实数根,
内没有实数根,
所以存在惟一的自然数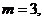 使得方程
使得方程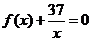 在区间
在区间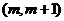 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。
变式:设f(x)=l―2x2,g(x)=x2-2x,若F(x)=则F(x)的最大值为__________.