摘要：变式:函数的图象与它的反函数图象所围成的面积是
网址：http://m.1010jiajiao.com/timu_id_524482[举报]
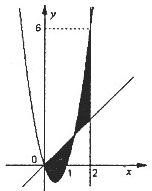如图，已知二次函数f（x）=ax2+bx+c，直线l1：x=2，直线l2：y=3tx（其中-1＜t＜1，t为常数）；若直线l2与函数f（x）的图象以及直线l1，l2与函数f（x）以及的图象所围成的封闭图形如阴影所示．（I）求y=f（x）；
（2）求阴影面积s关于t的函数y=s（t）的解析式．
已知二次函数f（x）=ax2+bx+c，满足f（0）=f（1）=0，且f（x）的最小值是-
．
（1）求f（x）的解析式；
（2）设直线l：y=t2-t（其中0＜t＜
，t为常数），若直线l与f（x）的图象以及y轴所围成封闭图形的面积是S1（t），直线l与f（x）的图象所围成封闭图形的面积是S2（t），设g(t)=S1(t)+
S2(t)，当g（t）取最小值时，求t的值．
（3）已知m≥0，n≥0，求证：
(m+n)2+
(m+n)≥m
+n
．
查看习题详情和答案>>
| 1 |
| 4 |
（1）求f（x）的解析式；
（2）设直线l：y=t2-t（其中0＜t＜
| 1 |
| 2 |
| 1 |
| 2 |
（3）已知m≥0，n≥0，求证：
| 1 |
| 2 |
| 1 |
| 4 |
| n |
| m |
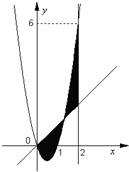如图，已知二次函数f（x）=ax2+bx+c，直线l1：x=2，直线l2：y=3tx（其中-1＜t＜1，t为数）；．若直线l2与函数f（x）的图象以及直线l1，l2与函数f（x）的图象所围成的封闭图形如阴影所示．（1）求y=f（x）；
（2）求阴影面积s关于t的函数y=s（t）的解析式；（3）若过点A（1，m），m≠4可作曲线y=s（t），t∈R的三条切线，求实数m的取值范围．
已知二次函数f（x）=ax2+bx+c，直线l1：x=2，l2：y=-t2+8t（其中0≤t≤2．t为常数）；若直线l1、l2与函数f（x）的图象以及l1，y轴与函数f（x）的图象所围成的封闭图形如阴影所示．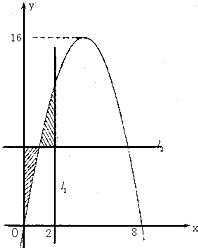
已知二次函数f（x）=ax2+bx+c，直线l1：y=-t2+8t（其中0≤t≤2．t为常数）；l2：x=2．若直线l1、l2与函数f（x）的图象以及l1，y轴与函数f（x）的图象所围成的封闭图形如阴影所示．