2007届广东省韶关市高三摸底考试理科数学试题
本试卷分第Ⅰ卷(选择题、填空题)和第Ⅱ卷解答题两部分,满分150分.考试用时间120分钟.
注意事项:
1.答第I卷前,考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答卷上;2.第I卷每小题得出答案后,请将答案填写在答题卷相应表格指定位置上。答在第Ⅰ卷上不得分;3.考试结束,考生只需将第Ⅱ卷(含答卷)交回。
参考公式:  , 其中
, 其中 是锥体的底面积,
是锥体的底面积, 是锥体的高.
是锥体的高.
第Ⅰ卷(选择题、填空题共70分)
一、选择题 (每小题5分,共40分)
1.下列各组两个集合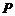 和
和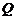 ,表示同一集合的是( )
,表示同一集合的是( )
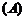
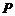 =
=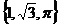 ,
,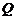 =
=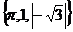
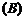
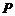 =
=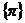 ,
,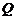 =
=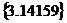
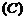
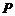 =
=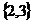 ,
,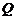 =
=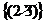

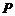 =
=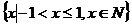 ,
,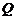 =
=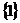
2.已知复数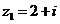 ,
,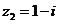 ,则
,则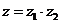 在复平面上对应的点位于( )
在复平面上对应的点位于( )
 第一象限
第一象限  第二象限
第二象限
 第三象限
第三象限  第四象限
第四象限
 3. 函数
3. 函数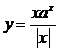
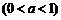 的图象的大致形状是
( )
的图象的大致形状是
( )
4.有关命题的说法错误的是 ( )
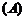 命题“若
命题“若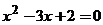 则
则
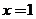 ”的逆否命题为:“若
”的逆否命题为:“若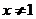 , 则
, 则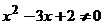 ”.
”.
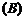 “
“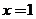 ”是“
”是“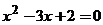 ”的充分不必要条件.
”的充分不必要条件.
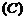 若
若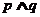 为假命题,则
为假命题,则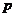 、
、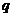 均为假命题.
均为假命题.
 对于命题
对于命题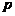 :
: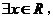 使得
使得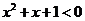 . 则
. 则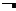
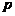 :
: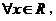 均有
均有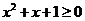 .
.
5. 已知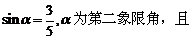
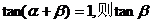 的值是
( )
的值是
( )
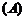

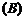 7
7

6.甲、乙、丙、丁四位同学各自对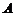 、
、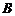 两变量的线性相关性作试验,并用回归分析方法分别求得相关系数
两变量的线性相关性作试验,并用回归分析方法分别求得相关系数 与残差平方和
与残差平方和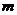 如下表:
如下表:
甲
乙
丙
丁

0.82
0.78
0.69
0.85
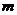
106
115
124
103
则哪位同学的试验结果体现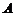 、
、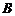 两变量更强的线性相关性?( )
两变量更强的线性相关性?( )

 甲
甲
 乙
乙
 丙
丙  丁
丁
7.如图,一个空间几何体的主视图、左视图、俯视图为全等
的等腰直角三角形,如果直角三角形的直角边长为1,那么这
个几何体的体积为 ( )
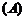 1
1 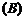
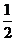
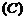
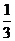

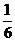
8.
已知公差不为零的等差数列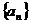 与等比数列
与等比数列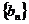 满足:
满足:
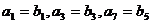 ,那么 ( )
,那么 ( )
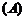
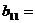
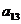
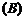
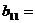
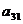
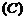
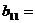
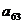

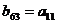
二.填空题(每小题5分,共30分)
9.已知向量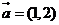 ,
,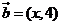 ,且
,且 ,则x= __________.
,则x= __________.
10.函数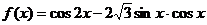 的最小正周期是 .
的最小正周期是 .
11.在约束条件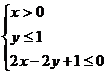 下,目标函数
下,目标函数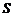 =
=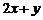 的最大值为
.
的最大值为
.
12..已知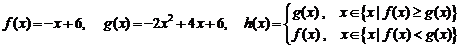 ,
,
则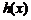 的最大值为
.
的最大值为
.
13.利用柯西不等式判断下面两个数的大小: 已知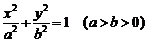 , 则
, 则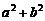 与
与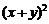 的大小关系,
的大小关系, 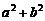
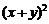 (用“
(用“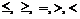 ”符号填写).
”符号填写).
14.在如下程序框图中,输入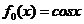 ,则输出的是__________
,则输出的是__________


2007届广东省韶关市高三摸底考试理科数学试题
学校______________ 学号____________ 姓名_______________ 得分_________
题号
1
2
3
4
5
6
7
8
答案
二、填空题答卷:
9.________________________. 10.__________________________.
11.________________________. 12.__________________________.
13.________________________. 14. ___________________________
题号
一
二
三
总分
15
16
17
18
19
20
分数
第Ⅱ解答题(共80分)
15. (本题满分12分)
在△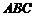 中,已知a、b、
中,已知a、b、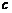 分别是三内角
分别是三内角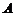 、
、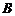 、
、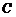 所对应的边长,且
所对应的边长,且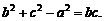
(Ⅰ)求角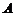 的大小;
的大小;
(Ⅱ)若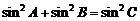 ,求角
,求角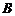 的大小.
的大小.
16. (本题满分12分)
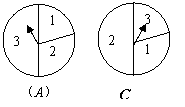
如图所示,
有两个独立的转盘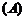 、
、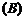 .两个图中三个扇形区域的圆心角分别为
.两个图中三个扇形区域的圆心角分别为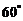 、
、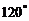 、
、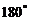 .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘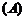 指针对的数为
指针对的数为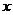 ,转盘
,转盘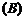 指针对的数为
指针对的数为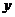 .设
.设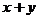 的值为
的值为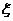 ,每转动一次则得到奖励分
,每转动一次则得到奖励分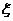 分.
分.
 (Ⅰ)求
(Ⅰ)求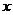 <2且
<2且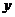 >1的概率;
>1的概率;
(Ⅱ) 某人玩12次,求他平均可以得到多少奖励分?
17.(本题满分14分)
如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=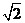 .
.
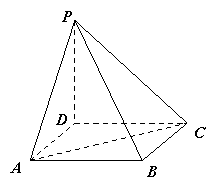 (Ⅰ)求证:PD⊥面ABCD;
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
 18.(本题满分14分)
18.(本题满分14分)
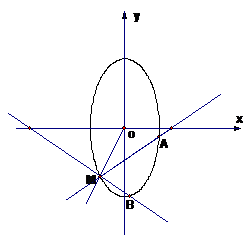
已知椭圆方程为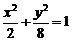 ,射线
,射线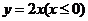 与椭圆的交点为
与椭圆的交点为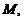 过
过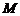 作倾斜角互补的两条直线,分别与椭圆交于
作倾斜角互补的两条直线,分别与椭圆交于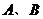 两点(异于
两点(异于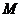 ).
).
(I)求证: 直线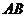 的斜率
的斜率 ;
;
(II)求△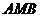 面积的最大值.
面积的最大值.
19.(本题满分14分)
在数列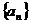 中,前
中,前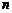 项和为
项和为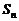 .已知
.已知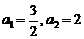 且
且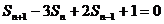 (
(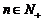 , 且
, 且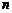
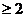 ).
).
(Ⅰ)求数列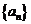 的通项公式;
的通项公式;
(Ⅱ) 求数列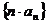 的前
的前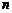 项和
项和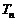 .
.
20. (本题满分14分)
已知二次函数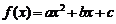 , 满足
, 满足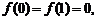 且
且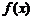 的最小值是
的最小值是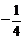 .
.
(Ⅰ)求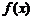 的解析式;
的解析式;
(Ⅱ)设直线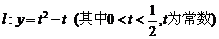 ,若直线
,若直线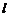 与
与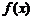 的图象以及
的图象以及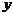 轴所围
轴所围
成封闭图形的面积是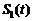 , 直线
, 直线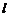 与
与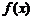 的图象所围成封闭图形的面积是
的图象所围成封闭图形的面积是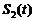 ,
,
设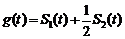 ,当
,当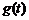 取最小值时,求
取最小值时,求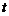 的值.
的值.
(Ⅲ)已知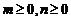 , 求证:
, 求证: 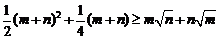 .
.
2007届广东省韶关市高三摸底考试理科数学试题
答案及评分标准
ADDCB DDC
题号
9
10
11
12
13
14
答案
2
二、填空题
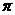
2
6
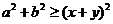
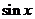
三、解答题
15解:(Ⅰ)在△ABC中,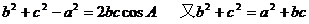
 …………6分
…………6分
(Ⅱ)由正弦定理,又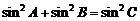 ,故
,故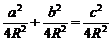 …………8分
…………8分
即: 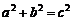 故△ABC是以角C为直角的直角三角形……………10分
故△ABC是以角C为直角的直角三角形……………10分
又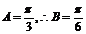 …………………………………………………………12分
…………………………………………………………12分
16.解:(Ⅰ)由几何概率模型可知:P(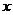 =1)=
=1)=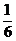 、P(
、P(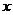 =2)=
=2)=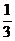 、P(
、P(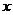 =3)=
=3)=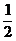 ;
;
P(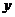 =1)=
=1)=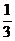 、P(
、P(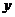 =2)=
=2)=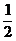 、P(
、P(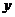 =3)=
=3)=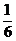 …………………………………………….2分
…………………………………………….2分
则P(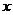 <2)=
P(
<2)=
P(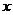 =1)=
=1)=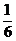 ,P(
,P(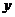 >1)=
P(
>1)=
P(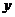 =2)+
P(
=2)+
P(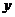 =3)=
=3)=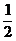 +
+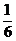 =
=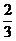
所以P(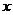 <2且
<2且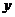 >1)=
P(
>1)=
P(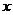 <2)
<2)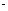 P(
P(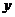
>1)=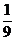 …………………………………….6分
…………………………………….6分
(Ⅱ)由条件可知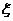 的取值为:2、3、4、5、6. 则
的取值为:2、3、4、5、6. 则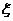 的分布列为:
的分布列为:
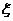
2
3
4
5
6
P
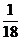
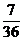
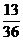
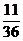
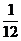
…………………………………………………………………………………………………………………………………………………………..………10分
他平均一次得到的钱即为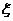 的期望值:
的期望值:
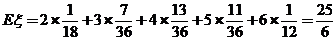
所以给他玩12次,平均可以得到 分..……………………………………………………..12分
分..……………………………………………………..12分
17. (Ⅰ)证明: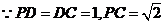 ,
,
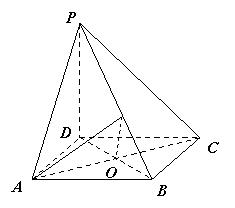
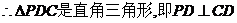 .……2分
.……2分
又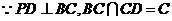 ,……4分
,……4分
∴ PD⊥面ABCD………6分
(Ⅱ)解:连结BD,设BD交AC于点O,
过O作OE⊥PB于点E,连结AE,
∵PD⊥面ABCD, ∴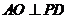 ,
,
又∵AO⊥BD, ∴AO⊥面PDB.
∴AO⊥PB,
∵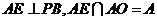 ,
,
∴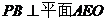 ,从而
,从而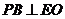 ,
,
故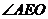 就是二面角A-PB-D的平面角.……………………10分
就是二面角A-PB-D的平面角.……………………10分
∵ PD⊥面ABCD, ∴PD⊥BD,
∴在Rt△PDB中, 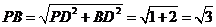 ,
,
又∵ , ∴
, ∴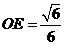 ,………………………………………12分
,………………………………………12分
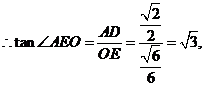 ∴
∴ 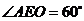 .…………………14分
.…………………14分
故二面角A-PB-D的大小为60°.
18.本题主要考查椭圆的标准方程和几何性质、直线方程、直线与方程的位置关系等解析几何的基础知识和基本思想方法,考察推理及运算能力。
(1)∵ 斜率
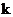 存在,不妨设
存在,不妨设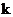 >0,求出
>0,求出 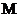 (
(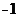 ,
,  ).
). 1分
1分
直线 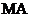 方程为
方程为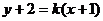 ,直线
,直线  方程
方程 
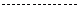 2分
2分
分别与椭圆方程联立,可解出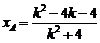 ,
,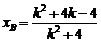
 5分
5分
∴ 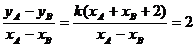 .
.
∴ 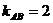 .
.
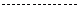 7分
7分
(2)设直线AB方程为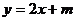 ,与
,与 联立,消去y得
联立,消去y得
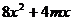
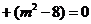 .
.
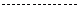 9分
9分
由 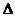 >0得-4<
>0得-4< 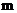 <4,且
<4,且 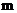 ≠0,
≠0,
点
 到
到 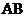 的距离为
的距离为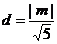 .
.
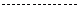 10分
10分
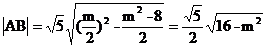
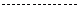 11分
11分
设△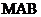 的面积为S. ∴
的面积为S. ∴ 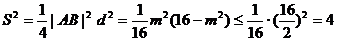 .
.
当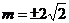 时,得
时,得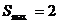 .
.
 14分
14分
19.解:(1).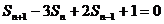 (n
(n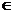 N+ , 且n
N+ , 且n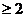 )…………①
)…………①
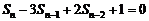 (n
(n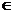 N+ , 且n
N+ , 且n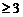 )………………………②
)………………………②
①-②得: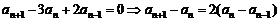 ………3分
………3分
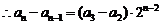
又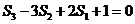 ,
∴
,
∴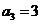
故: 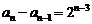

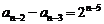
……………………
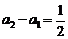
上列各式相加得: 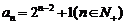
(2).由n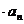 =
=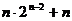 得
得
Tn=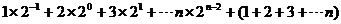
令An=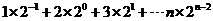
则2 An=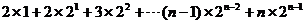 ………9分
………9分
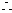 An=
An=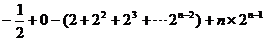 ……………10分
……………10分
=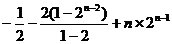
=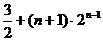 - ---------------------------------11分
- ---------------------------------11分
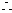 Tn=
Tn=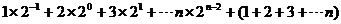
=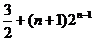 +
+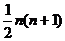 ----------------------------------14分
----------------------------------14分
20.解: (1)由二次函数图象的对称性, 可设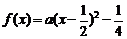 ,又
,又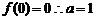
故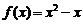 …………………3分
…………………3分
(2) 据题意, 直线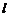 与
与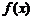 的图象的交点坐标为
的图象的交点坐标为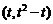 ,由定积分的几何意义知
,由定积分的几何意义知
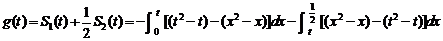 ………5分
………5分
=
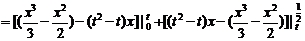
=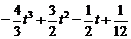 …………………………………………………………7分
…………………………………………………………7分
而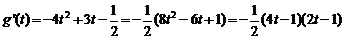
令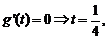 或
或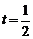 (不合题意,舍去)
(不合题意,舍去)
当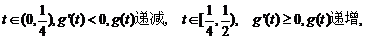 ……………8分
……………8分
故当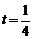 时,
时,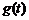 有最小值.………………………………………………………9分
有最小值.………………………………………………………9分
(3) 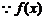 的最小值为
的最小值为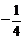
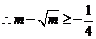 ……①
……①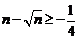 ……②……………………………11分
……②……………………………11分
①+②得: 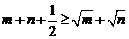 ………③
………③
又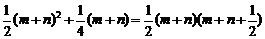 …………………12分
…………………12分
由均值不等式和③知:
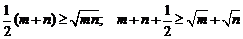 …………………………13分
…………………………13分
故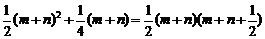
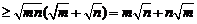 ……14分
……14分