摘要:解:(1). (nN+ , 且n)----①
网址:http://m.1010jiajiao.com/timu_id_25623[举报]
| |||||||||||
已知函数f(x)=ax2+bx+c满足:f(1)=3,且f(x)在R上为奇函数.
(1)求函数f(x)的解析式;
(2)设Sn=f(
)+f(
)+f(
)+…+f(
),若不等式
<
对n∈N+恒成立,求实数m的取值范围;
(3)若数列{an},{bn}满足:a1=1,an+1=
;b1=1,bn+1-bn=
,记g(n)=
,问是否存在k∈N,使g(k+1)=2g(k)成立,若存在,求出k值;若不存在,说明理由.
查看习题详情和答案>>
(1)求函数f(x)的解析式;
(2)设Sn=f(
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n |
| n |
| mn |
| Sn |
| mn+1 |
| Sn+1 |
(3)若数列{an},{bn}满足:a1=1,an+1=
| f(an) |
| 2f(an)+3 |
| 1 |
| an |
|
已知数列{an}及fn(x)=a1x+a2x2+…+anxn, fn(-1)=(-1)nn,n=1,2,3,…,
(1)求 a1, a2, a3的值;
(2)求数列{an}的通项公式;
(3)求证: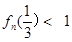 .
.
【解析】本试题主要是考查了数列中归纳猜想的原理,意义运用函数关系求解数列的通项公式,并且运用错位相减法求解数列的和的数学思想。
查看习题详情和答案>>
已知函数f(x)=ex-x(e为自然对数的底数)
(Ⅰ)求f(x)的最小值;
(Ⅱ)设不等式f(x)>ax的解集为P,且{x|0≤x≤2}⊆P,求实数a的取值范围;
(Ⅲ)设n∈N*,证明:(
)n+(
)n+…+(
)n+(
)n<
.
查看习题详情和答案>>
(Ⅰ)求f(x)的最小值;
(Ⅱ)设不等式f(x)>ax的解集为P,且{x|0≤x≤2}⊆P,求实数a的取值范围;
(Ⅲ)设n∈N*,证明:(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| 1 |
| 1-e-1 |
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
已知矩阵M=
,N=
(Ⅰ)求矩阵NN;
(Ⅱ)若点P(0,1)在矩阵M对应的线性变换下得到点P′,求P′的坐标.
(2)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程是
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的极坐标方程是ρ=2cosθ(Ⅰ)在直角坐标系xOy中,求圆C的直角坐标方程
(Ⅱ)求圆心C到直线l的距离.
(3)选修4-5:不等式选讲
已知函数f(x)=|x-1|
(Ⅰ)解不等式f(x)>2;
(Ⅱ)求函数y=f(-x)+f(x+5)的最小值.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
已知矩阵M=
|
|
(Ⅰ)求矩阵NN;
(Ⅱ)若点P(0,1)在矩阵M对应的线性变换下得到点P′,求P′的坐标.
(2)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程是
|
(Ⅱ)求圆心C到直线l的距离.
(3)选修4-5:不等式选讲
已知函数f(x)=|x-1|
(Ⅰ)解不等式f(x)>2;
(Ⅱ)求函数y=f(-x)+f(x+5)的最小值.