题目内容
2．
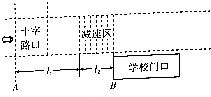为了安全，学校校门前马路一般有限速标志，如图所示，为一学校门口前面马路的俯视图，绿灯时，在十字路口A线处有一轿车（可视为质点）从静止开始故匀加速直线运动，轿车的最大启动加速度为10m/s2，距A线l1=500m处有一减速区，减速区宽度l2=15m，在减速区能达到的加速度数值足够大，设学校门口限速36km/h，市区内轿车限速72km/h．要求轿车从进入减速区时开始减速，减速时视为做匀减速直线运动．在不违规的情况下，试求轿车从A开始启动到学校门口B的最短时间．
分析 汽车在进入减速区前，汽车先加速后匀速，求得经历的时间，进入减速区后，以最小的加速度减速，到达学校门口所需时间最短，根据速度时间公式和速度位移公式即可求得
解答 解：v限=36km/h=10m/s，vm=72km/h=20m/s
在加速阶段，到达最大速度所需时间为t1，则有：${t}_{1}=\frac{{v}_{m}}{{a}_{1}}=\frac{20}{10}s=2s$
2s内通过的位移为：${x}_{1}=\frac{1}{2}{{a}_{1}t}_{1}^{2}=\frac{1}{2}×10×{2}^{2}m=20m$
达到最大速度后匀速运动，匀速运动的时间为：${t}_{2}=\frac{{l}_{1}-{x}_{1}}{{v}_{m}}=\frac{500-20}{20}s=24s$
进入减速区后，减速运动，设加速度为a，则有：v限=vm+at
$2a{l}_{2}{=v}_{限}^{2}{-v}_{m}^{2}$
代入数据解得：t=1s
故经历的总时间为：t总=t1+t2+t=27s
答：轿车从A开始启动到学校门口B的最短时间为27s．
点评 本题主要考查了匀变速直线运动，明确各阶段的运动过程，知道如何运动时间最短，即在减速阶段以最小的加速度减速运动时间最短
练习册系列答案
相关题目
12．
如图所示，质量均为m的A、B两物体叠放在竖直轻质弹簧并保持静止，用大小等于$\frac{1}{2}$mg的恒力F竖直向上拉B，当上升距离为h时B与A开始分离．下列说法正确的是（ ）
如图所示，质量均为m的A、B两物体叠放在竖直轻质弹簧并保持静止，用大小等于$\frac{1}{2}$mg的恒力F竖直向上拉B，当上升距离为h时B与A开始分离．下列说法正确的是（ ）| A． | B与A刚分离时，弹簧为原长 | |
| B． | B与A刚分离时，A的速度达到最大 | |
| C． | 弹簧的劲度系数等于$\frac{3mg}{2h}$ | |
| D． | 从开始运动到B与A刚分离的过程中，B物体的动能先增大后减小 |
10．
一台理想变压器的原、副线圈的匝数比是5：1，原线圈接入电压为220V的正弦交流电，各元件正常工作，一只理想二极管和一个滑动变阻器R串联接在副线圈上，如图所示，电压表和电流表均为理想交流电表．则下列说法正确的是（ ）
一台理想变压器的原、副线圈的匝数比是5：1，原线圈接入电压为220V的正弦交流电，各元件正常工作，一只理想二极管和一个滑动变阻器R串联接在副线圈上，如图所示，电压表和电流表均为理想交流电表．则下列说法正确的是（ ）| A． | 原、副线圈中的电流之比为5：1 | |
| B． | 电压表的读数约为31.11V | |
| C． | 若滑动变阻器接入电路的阻值为20Ω，则1分钟内产生的热量约为2.9×103J | |
| D． | 若将滑动变阻器的滑片向上滑动，则两电表读数均减小 |
7．下列关于电场强度的说法中，正确的是（ ）
| A． | 公式E=$\frac{F}{q}$只适用于真空中点电荷产生的电场 | |
| B． | 由公式E=$\frac{F}{q}$ 可知，电场中某点的电场强度E与试探电荷q在电场中该点所受的电场力成正比 | |
| C． | 在公式F=k$\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}$ 中，k$\frac{{Q}_{2}}{{r}^{2}}$ 是点电荷Q2 产生的电场在点电荷Q1处的场强大小；而k$\frac{{Q}_{1}}{{r}^{2}}$ 是点电荷Q 1 产生的电场在点电荷Q2处场强的大小 | |
| D． | 由公式E=k$\frac{Q}{{r}^{2}}$ 可知，在离点电荷非常近的地方（r→0），电场强度E可达无穷大 |
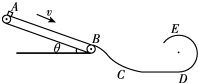如图所示，传送带A、B之间的距离L=3.2m，与水平面夹角θ=37°，传送带沿顺时针方向转动，速度恒为v=2m/s，在上端A点无初速度放置一个质量为m=1kg、大小可视为质点的金属块，它与传送带的动摩擦因数为μ=0.5，金属块滑离传送带后经过弯道沿半径R=0.4m的光滑圆轨道做圆周运动，刚好能通过最高点E，已知B、D两点的竖直高度差为h=0.5m（g取10m/s2）．求：
电磁弹射器是航空母舰上的一种舰载机起飞装置，已由美国福特号航母首先装备，我国未来的航母将采用自行研制的电磁弹射器．电磁弹射系统包括电源、强迫储能装置、导轨和脉冲发生器等等．其工作原理可简化为如图所示；上下共4根导轨，飞机前轮下有一牵引杆，与飞机前轮连为一体，可收缩并放置在飞机的腹腔内．起飞前牵引杆伸出至上下导轨之间，强迫储能装置提供瞬发能量，强大的电流从导轨流经牵引杆，牵引杆在强大的安培力作用下推动飞机运行到高速．现有一弹射器弹射某飞机，设飞机质量m=2×104kg，起飞速度为v=60m/s，起飞过程所受到阻力恒为机重的0.2倍，在没有电磁弹射器的情况下，飞机从静止开始匀加速起飞，起飞距离为l=200m，在电磁弹射器与飞机的发动机（设飞机牵引力不变）同时工作的情况下，匀加速起飞距离减为50m，假设弹射过程强迫储能装置的能量全部转为飞机的动能．取g=10m/s2．求：