题目内容
9.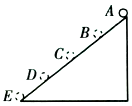 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中错误的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中错误的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点经历的时间tB:tC:tD:tE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 物体从A 运动到E全过程的平均速度$\overline{v}$=vB | |
| D. | 物体通过每一部分时,其速度增量均相等 |
分析 A、根据v2=2ax,可求出物体到达各点的速度之比.
B、初速度为零的匀加速运动的推论:tB:tC:tD:tE=$1:\sqrt{2}:\sqrt{3}:\sqrt{4}$根据这个结论判断时间关系.
C、物体从A运动到E的全过程平均速度等于中间时刻的瞬时速度.
D、看每一段位移所用的时间是否相同去判断速度的增量关系.
解答 解:A、初速度为零的匀加速运动的推论:tB:tC:tD:tE=$1:\sqrt{2}:\sqrt{3}:\sqrt{4}$,物体到达各点的速率之比为1:$\sqrt{2}$:$\sqrt{3}$:$\sqrt{4}$,故A正确
B、因为v=at,初速度为零的匀加速运动的推论:tB:tC:tD:tE=$1:\sqrt{2}:\sqrt{3}:\sqrt{4}$,物体到达各点的速率之比为1:$\sqrt{2}$:$\sqrt{3}$:$\sqrt{4}$,故物体到达各点所经历的时间${t}_{E}=2{t}_{B}=\sqrt{2}{t}_{C}=\frac{2}{\sqrt{3}}{t}_{D}$,故B正确
C、物体从A运动到E的全过程平均速度等于中间时刻的瞬时速度,即等于经过B点时的瞬时速度,故C正确
D、物体通过每一部分时,所用时间不同,故其速度增量不同物体从A运动到E的全过程平均速度等于中间时刻的瞬时速度,不是中间位移的瞬时速度,故D错误
本题选择错误的,故选:D
点评 解决本题的关键掌握速度位移公式v2-v02=2ax,以及知道某段时间内的平均速度等于中间时刻的瞬时速度.

练习册系列答案
相关题目
19.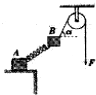 如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
 如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )| A. | 木块A对桌面的压力 | B. | 弹簧与水平方向的夹角 | ||
| C. | 木块A与桌面之间的动摩擦因数 | D. | 弹簧的形变量 |
14.如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置(x)-时间(t)图线.由图可知( )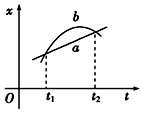

| A. | 在t1时刻,a、b两车相遇 | |
| B. | 在t2时刻,a、b两车运动方向相同 | |
| C. | 在t1到t2这段时间内,b车的速率先减小后增大 | |
| D. | 在t1到t2这段时间内,b车的速率一直比a车的大 |
1.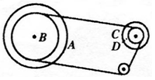 变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
 变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
变速自行车靠变换齿轮组合来改变行驶速度.如图所示是某一变速自行车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )| A. | 该自行车可变换两种不同挡位 | |
| B. | 该自行车可变换六种不同挡位 | |
| C. | 当A轮与D轮组合时,两轮的角速度之比ωA:ωD=1:4 | |
| D. | 当A轮与D轮组合时,两轮的角速度之比ωA:ωD=4:1 |
13.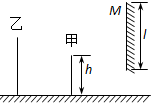 如图所示,M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍.二人略错开,以使乙能看到甲的像.用l表示镜的长度,h表示甲的身高,为使乙能看到镜中甲的全身像,l的最小值为( )
如图所示,M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍.二人略错开,以使乙能看到甲的像.用l表示镜的长度,h表示甲的身高,为使乙能看到镜中甲的全身像,l的最小值为( )
 如图所示,M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍.二人略错开,以使乙能看到甲的像.用l表示镜的长度,h表示甲的身高,为使乙能看到镜中甲的全身像,l的最小值为( )
如图所示,M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍.二人略错开,以使乙能看到甲的像.用l表示镜的长度,h表示甲的身高,为使乙能看到镜中甲的全身像,l的最小值为( )| A. | $\frac{1}{2}$h | B. | $\frac{2}{3}$h | C. | $\frac{3}{4}$h | D. | h |
 如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定于高度为H的光滑水平细杆A、B上,b球与B点距离为L,质量为4m的a球置于地面上,质量为m的b球从水平位置静止释放.
如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定于高度为H的光滑水平细杆A、B上,b球与B点距离为L,质量为4m的a球置于地面上,质量为m的b球从水平位置静止释放.