题目内容
20. 如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定于高度为H的光滑水平细杆A、B上,b球与B点距离为L,质量为4m的a球置于地面上,质量为m的b球从水平位置静止释放.
如图所示,一根不可伸长的轻绳两端各系一个小球a和b,跨在两根固定于高度为H的光滑水平细杆A、B上,b球与B点距离为L,质量为4m的a球置于地面上,质量为m的b球从水平位置静止释放.(1)a球对地面的最小压力为多大?
(2)b球向下摆动的角度θ为多大时重力对b球做功的功率最大
(3)已知细线能承受的最大拉力为Fm,现给b球竖直向下的初速度,当b球运动到B正下方时细线恰被拉断,求b球落地点与B点的距离.
分析 (1)当b球摆到最低点时,拉力最大,a球对地面的压力最小,根据动能定理和牛顿第二定理求出最大拉力,对a球分析,根据平衡求出最小支持力,从而得出最小压力.
(2)根据动能定理求出b球摆到角度θ时的速度,结合瞬时功率的公式求出重力的瞬时功率表达式,根据数学知识得出θ为多大时,功率最大.
(3)根据牛顿第二定律求出小球在最低点的速度,结合平抛运动的时间求出水平位移,根据平行四边形定则求出b球落地点与B点的距离.
解答 解:(1)当b球摆到最低点时,绳子的拉力最大,a球对地面的压力最小.
根据动能定理得,mgL=$\frac{1}{2}m{v}^{2}$,解得v=$\sqrt{2gL}$,
根据牛顿第二定律得,F-mg=m$\frac{{v}^{2}}{L}$,解得F=3mg,
对a球分析,根据平衡有F+N=4mg,解得N=mg,
根据牛顿第三定律知,a球对地面的最小压力为mg.
(2)向下摆动的角度为θ时,根据动能定理得,$mgLsinθ=\frac{1}{2}m{v}^{2}$,解得v=$\sqrt{2gLsinθ}$,
则重力的瞬时功率P=mgvcosθ=mg$\sqrt{2gLsinθ}$cosθ,
根据数学知识得,当sinθ=$\frac{\sqrt{3}}{3}$时,P有最大值,θ=arcsin$\frac{\sqrt{3}}{3}$.
(3)b球在最低点,根据牛顿第二定律有:${F}_{m}-mg=m\frac{{v}^{2}}{L}$,解得v=$\sqrt{\frac{({F}_{m}-mg)L}{m}}$,
平抛运动的时间$t=\sqrt{\frac{2(H-L)}{g}}$,
平抛运动的水平位移x=vt=$\sqrt{\frac{2(H-L)({F}_{m}-mg)L}{mg}}$,
b球落地点与B点的距离s=$\sqrt{{x}^{2}+(H-L)^{2}}$=$\sqrt{\frac{2(H-L)({F}_{m}-mg)L}{mg}+(H-L)^{2}}$.
答:(1)a球对地面的最小压力为mg;
(2)b球向下摆动的角度θ为arcsin$\frac{\sqrt{3}}{3}$时,重力对b球做功的功率最大;
(3)b球落地点与B点的距离为$\sqrt{\frac{2(H-L)({F}_{m}-mg)L}{mg}+(H-L)^{2}}$.
点评 本题考查了圆周运动和平抛运动的综合运动员,知道平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源是解决本题的关键.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案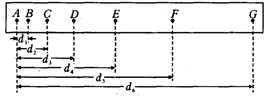
| 速度/m•s-1 | 0.122 | 0.164 | 0.205 | 0.250 | 0.289 |
| 对应点 | B | C | D | E | F |
(2)并求物体的加速度a=0.42m/s2;.
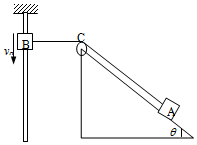 如图所示,轻质不可伸长的细绳,绕过光滑定滑轮C,与质量为m的物体A连接,A放在倾角为θ的光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接.现BC连线恰沿水平方向,从当前位置开始B以速度v0匀速下滑.设绳子的张力为T,在此后的运动过程中,下列说法正确的是( )
如图所示,轻质不可伸长的细绳,绕过光滑定滑轮C,与质量为m的物体A连接,A放在倾角为θ的光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接.现BC连线恰沿水平方向,从当前位置开始B以速度v0匀速下滑.设绳子的张力为T,在此后的运动过程中,下列说法正确的是( )| A. | 物体A做匀速运动 | B. | 物体A做加速运动 | C. | T可能小于mgsinθ | D. | T一定大于mgsinθ |
| A. | 曲线运动一定是变速运动 | |
| B. | 曲线运动的物体速度大小一定变化 | |
| C. | 曲线运动的物体所受合外力一定变化 | |
| D. | 曲线运动的加速度一定变化 |
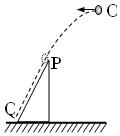 如图,不计空气阻力,从O点水平抛出的小球抵达光滑斜面上端P处时,速度方向恰好沿着斜面方向,然后紧贴斜面PQ做匀加速直线运动.下列说法正确的是( )
如图,不计空气阻力,从O点水平抛出的小球抵达光滑斜面上端P处时,速度方向恰好沿着斜面方向,然后紧贴斜面PQ做匀加速直线运动.下列说法正确的是( )| A. | 小球在斜面上运动的加速度大小比平抛运动时的大 | |
| B. | 小球在斜面运动的过程中地面对斜面的支持力大于小球和斜面的总重 | |
| C. | 撤去斜面,小球仍从O点以相同速度水平抛出,落地速率将变大 | |
| D. | 撤去斜面,小球仍从O点以相同速度水平抛出,落地时间将减小 |
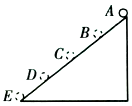 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中错误的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中错误的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点经历的时间tB:tC:tD:tE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 物体从A 运动到E全过程的平均速度$\overline{v}$=vB | |
| D. | 物体通过每一部分时,其速度增量均相等 |
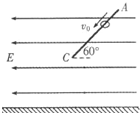 如图所示,在水平向左的匀强电场中有一表面光滑、与水平成60°角的绝缘直杆AC,其下端C距离地面有一定高度.一质量为0.5kg的带电小环套在直杆上,以某一速度沿杆匀速下滑.不计空气阻力,重力加速度g=10m/s2.则下列说法正确的是( )
如图所示,在水平向左的匀强电场中有一表面光滑、与水平成60°角的绝缘直杆AC,其下端C距离地面有一定高度.一质量为0.5kg的带电小环套在直杆上,以某一速度沿杆匀速下滑.不计空气阻力,重力加速度g=10m/s2.则下列说法正确的是( )| A. | 小环带正电 | |
| B. | 小环受到的电场力大小为10N | |
| C. | 小环离开直杆后做类平抛运动 | |
| D. | 小环在地面上的落点不可能在C点正下方 |
 在真空中一条直线上固定有三个点电荷qA=-8×10-9C,qB=5×10-9C,qC=4×10-9C,AB=10cm,BC=6cm.如图所示,求qB受到的库仑力的大小和方向.
在真空中一条直线上固定有三个点电荷qA=-8×10-9C,qB=5×10-9C,qC=4×10-9C,AB=10cm,BC=6cm.如图所示,求qB受到的库仑力的大小和方向.