题目内容
12.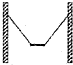 如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为√65m木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为√65m木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )| A. | F1增大,F2增大 | B. | F1不变,F2增大 | C. | F1不变,F2减小 | D. | F1不变,F2不变 |
分析 木板静止时,受重力和两个拉力而平衡,根据共点力平衡条件并结合正交分解法列式分析即可.
解答  解:木板静止时,受重力和两个拉力而平衡,
解:木板静止时,受重力和两个拉力而平衡,
故三个力的合力为零,即:F1=0;
由于两段绳子的长度相等,所以绳子与绳子方向的夹角是相等的,根据共点力平衡条件,有:2F2cosθ=mg
其中由几何关系可得:sinθ=3d−d22d=12
解得:F2=mg2cosθ=mg√3
当用另一块长为2d,质量为√65m木板将原木板换掉后,绳子与竖直方向的夹角θ减小,
则sinθ′=3d−2d22d=14
所以:cosθ′=√154
F2′=m′2cosθ′=√65mg2×√154=√245√3mg<F2选项C正确.
故选:C
点评 本题是简单的三力平衡问题,关键是受力分析后运用图示法分析,不难.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.在同一地点,甲、乙两物体沿同一方向做直线运动的速度-时间图象如图所示,则( ) 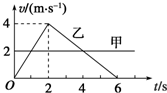

| A. | 两物体两次相遇的时刻是2 s末和6 s末 | |
| B. | 4 s后甲在乙后面 | |
| C. | 两物体相距最远的时刻是2 s末 | |
| D. | 乙物体先向前运动2 s,随后向后运动 |
7.某人站在20m的平台边缘,以20m/s的初速度竖直上抛一石子,不计空气阻力,g=10m/s2,则抛出后石子距离抛出点15m处的时间是( )
| A. | 1s | B. | 3s | C. | (√7-2)s | D. | (√7+2)s |
17.下列说法正确的是( )
| A. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| B. | “闻其声而不见其人”现象说明遇到同样障碍物时声波比可见光容易发生衍射 | |
| C. | 用超声波被血流反射回来其频率发生变化可测血流速度,这是利用多普勒效应 | |
| D. | 在双缝干涉实验中,用紫光代替黄光作为入射光可增大干涉条纹的间距 | |
| E. | 机械波和电磁波都可以在真空中传播 |
4.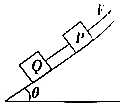 如图所示,有材料相同的P、Q两物块通过轻绳相连,并在拉力F作用下沿斜面向上运动,轻绳与拉力F的方向均平行于斜面.当拉力F一定时,Q受到绳的拉力( )
如图所示,有材料相同的P、Q两物块通过轻绳相连,并在拉力F作用下沿斜面向上运动,轻绳与拉力F的方向均平行于斜面.当拉力F一定时,Q受到绳的拉力( )
 如图所示,有材料相同的P、Q两物块通过轻绳相连,并在拉力F作用下沿斜面向上运动,轻绳与拉力F的方向均平行于斜面.当拉力F一定时,Q受到绳的拉力( )
如图所示,有材料相同的P、Q两物块通过轻绳相连,并在拉力F作用下沿斜面向上运动,轻绳与拉力F的方向均平行于斜面.当拉力F一定时,Q受到绳的拉力( )| A. | 与斜面倾角θ有关 | B. | 与摩擦因数有关 | ||
| C. | 与系统运动状态有关 | D. | 仅与两物块质量有关 |
1.一个质子和一个中子聚变结合成一个氘核,同时辐射一个γ光子.已知质子、中子、氘核的质量分别为m1、m2、m3,普朗克常量为h,真空中的光速为c.下列说法正确的是( )
| A. | 核反应方程是11H+10n→31H+γ | |
| B. | 聚变反应中的质量亏损△m=m1+m2-m3 | |
| C. | 辐射出的γ光子的能量E=(m1+m2-m3)c2 | |
| D. | γ光子的波长λ=hm1+m2+m3c2 |
