题目内容
20.一辆汽车从静止开始做匀加速直线运动,3s后速度达到12m/s(1)求加速过程中加速度的大小;
(2)若汽车在第3s末开始刹车.刹车的加速度大小为6m/s2,求从刹车开始1s时及10s时汽车的速度和运动的位移;
(3)求整个运动过程汽车的位移.
分析 (1)根据速度时间公式求出汽车加速过程中的加速度大小.
(2)根据速度时间公式求出汽车速度减为零的时间,判断汽车是否停止,再结合速度公式和位移公式求出汽车的速度和位移.
(3)根据速度位移公式求出匀减速直线运动的位移,结合匀加速直线运动的位移,从而得出总位移.
解答 解:(1)汽车加速过程中的加速度大小为:a=$\frac{{v}_{1}}{{t}_{1}}=\frac{12}{3}m/{s}^{2}=4m/{s}^{2}$,
(2)汽车速度减为零的时间为:${t}_{0}=\frac{0-{v}_{1}}{{a}_{2}}=\frac{-12}{-6}s=2s$,
则刹车开始1s时的速度为:v2=v1+a2t=12-6×1m/s=6m/s,
汽车的位移为:${x}_{2}={v}_{1}t+\frac{1}{2}{a}_{2}{t}^{2}=12×1-\frac{1}{2}×6×1$m=9m.
刹车后10s时的速度为零,运动的位移为:${x}_{3}=\frac{{0-{v}_{1}}^{2}}{2{a}_{2}}=\frac{-144}{-12}m=12m$.
(3)整个运动过程汽车的位移为:x=$\frac{{v}_{1}}{2}{t}_{1}+{x}_{3}=\frac{12}{2}×3+12$m=30m.
答:(1)加速过程中加速度的大小为4m/s2;
(2)刹车开始1s时的速度为6m/s,汽车的位移为9m.
(3)整个运动过程汽车的位移为30m.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,注意第二问为刹车问题,汽车速度减为零后不再运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.小车从A地开往D地,其s-t图象如图所示,其中BC段平行于时间轴,则下列说法正确的是( )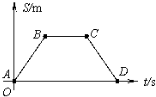

| A. | 小车在AB段做匀加速直线运动 | |
| B. | 小车在BC段处于静止状态 | |
| C. | 小车在CD段做匀减速直线运动 | |
| D. | 小车在到达D地的前一时刻的速度为零 |
11.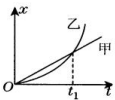 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的x-t图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的x-t图象如图所示,则下列说法正确的是( )
 甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的x-t图象如图所示,则下列说法正确的是( )
甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的x-t图象如图所示,则下列说法正确的是( )| A. | t1时刻两车位移相同 | |
| B. | t1时刻两车相距最远 | |
| C. | t1时刻两车的速度刚好相等 | |
| D. | 0到t1时间内,乙车的平均速度等于甲车的平均速度 |
15.两物体都做匀变速直线运动,在相同的时间间隔内,下列判断正确的是( )
| A. | 加速度越大的物体,速度改变越多 | |
| B. | 初速度越大的物体,位移一定越大 | |
| C. | 末速度越大的物体,位移一定越大 | |
| D. | 平均速度越大的物体,位移一定越大 |
12.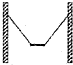 如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
 如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )| A. | F1增大,F2增大 | B. | F1不变,F2增大 | C. | F1不变,F2减小 | D. | F1不变,F2不变 |
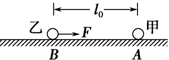 如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点间的距离为l0,释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=k$\frac{4Qq}{l_0^2}$(k为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.
如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点间的距离为l0,释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=k$\frac{4Qq}{l_0^2}$(k为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.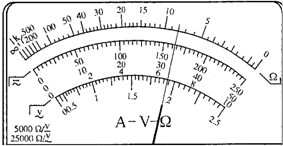 某一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测某一未知电阻的阻值.当用×100Ω挡测量时,发现指针的偏转角度很小.为了使测量结果更准确,测量前应进行如下两项操作:先换用×1000挡(填“×10”或“×1000”),接着进行欧姆调零(填“机械调零”或“欧姆调零”),然后再进行测量并读数.下图为一正在测量中的多用电表表盘.
某一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测某一未知电阻的阻值.当用×100Ω挡测量时,发现指针的偏转角度很小.为了使测量结果更准确,测量前应进行如下两项操作:先换用×1000挡(填“×10”或“×1000”),接着进行欧姆调零(填“机械调零”或“欧姆调零”),然后再进行测量并读数.下图为一正在测量中的多用电表表盘.
 如图所示,电源电动势为E,内阻为r,外电路总电阻为R,当S闭合后,电源总功率为$\frac{{E}^{2}}{R+r}$,电源的输出功率为$\frac{{E}^{2}R}{(R+r)^{2}}$,外电路消耗的功率为$\frac{{E}^{2}R}{(R+r)^{2}}$,内部消耗的功率为$\frac{{E}^{2}r}{(R+r)^{2}}$,电源的供电效率为$\frac{R}{R+r}$×100%.
如图所示,电源电动势为E,内阻为r,外电路总电阻为R,当S闭合后,电源总功率为$\frac{{E}^{2}}{R+r}$,电源的输出功率为$\frac{{E}^{2}R}{(R+r)^{2}}$,外电路消耗的功率为$\frac{{E}^{2}R}{(R+r)^{2}}$,内部消耗的功率为$\frac{{E}^{2}r}{(R+r)^{2}}$,电源的供电效率为$\frac{R}{R+r}$×100%.