题目内容
7.某人站在20m的平台边缘,以20m/s的初速度竖直上抛一石子,不计空气阻力,g=10m/s2,则抛出后石子距离抛出点15m处的时间是( )| A. | 1s | B. | 3s | C. | ($\sqrt{7}$-2)s | D. | ($\sqrt{7}$+2)s |
分析 距抛出点15m处有上下两个位置,通过上方15m处有向上通过和向下通过两种情况;根据匀变速直线运动的位移时间关系公式列式求解即可.
解答 解:竖直上抛运动是匀变速运动,当x=15m时,根据位移时间关系公式,有:
x=v0t-$\frac{1}{2}$gt2
解得:
t1=1s,t2=3s
当位移为x=-15m时,根据位移时间关系公式,有:
x=v0t-$\frac{1}{2}$gt2
解得:
t3=2+$\sqrt{7}$s,t4=2-$\sqrt{7}$s(舍去)
故选:ABD.
点评 本题关键是将竖直上抛运动的上升和下降阶段作为整个过程考虑(匀变速直线运动),同时要明确物体的位置可能在抛出点上方,也可能在抛出点下方.

练习册系列答案
相关题目
17.在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电源的频率为50Hz,记录小车运动的纸带如图1所示,在纸带上选择6个计数点A、B、C、D、E、F,相邻两计数点之间还有四个点未画出,各点到A点的距离依次是3.00cm、7.10cm、11.00cm、16.20cm、21.00cm.
(1)若只有这6个计数点,有那些计数点的瞬时速度不可测量A、F,根据所学知识可以求出AC的平均速度是0.355m/s.
(2)由纸带提供的数据求出打下点B、D瞬时速度
(3)根据表中的数据,在图2中作出小车运动的v-t图象:
(4)根据作出的v-t图线可得小车运动的加速度为0.50 m/s2.(保留两位有效数字)

(1)若只有这6个计数点,有那些计数点的瞬时速度不可测量A、F,根据所学知识可以求出AC的平均速度是0.355m/s.
(2)由纸带提供的数据求出打下点B、D瞬时速度
| 计数点序号 | B | C | D | E |
| 对应时刻t/s | 0.1 | 0.2 | 0.3 | 0.4 |
| 小车的速度v/(m•s-1) | 0.355 | 0.400 | 0.455 | 0.500 |
(4)根据作出的v-t图线可得小车运动的加速度为0.50 m/s2.(保留两位有效数字)
15.两物体都做匀变速直线运动,在相同的时间间隔内,下列判断正确的是( )
| A. | 加速度越大的物体,速度改变越多 | |
| B. | 初速度越大的物体,位移一定越大 | |
| C. | 末速度越大的物体,位移一定越大 | |
| D. | 平均速度越大的物体,位移一定越大 |
2.做匀变速直线运动的物体位移随时间的变化规律为x=24t-2t2(m),根据这一关系式可以知道,物体速度为零的时刻是( )
| A. | 2 s | B. | 6 s | C. | 12 s | D. | 24 s |
12.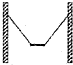 如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
 如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )
如图,用两根长均为2d的轻绳将长为d,质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点,制成一简易秋千.某次维修时用另一块长为2d,质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉,绳子的悬挂点还在木板的两端点,木板静止时,F1表示木板所受合力大小,F2表示单根轻绳对未板拉力的大小,则维修后( )| A. | F1增大,F2增大 | B. | F1不变,F2增大 | C. | F1不变,F2减小 | D. | F1不变,F2不变 |
19.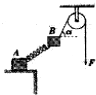 如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
 如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )
如图,质量分别为M、m的两个木块A、B通过轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态,绳与水平方向成α角.设最大静摩擦力等于滑动摩擦力,不计滑轮与绳间的摩擦.则可以求下列哪些量( )| A. | 木块A对桌面的压力 | B. | 弹簧与水平方向的夹角 | ||
| C. | 木块A与桌面之间的动摩擦因数 | D. | 弹簧的形变量 |
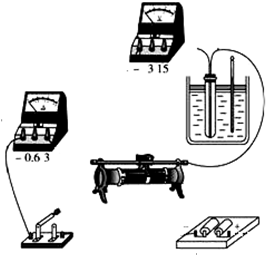 热敏电阻是传感电路中常用的电子元件.现用伏安法测绘出热敏电阻分别在温度为t1=45℃和温度为t2=75℃时的伏安特性曲线,要求特性曲线尽可能完整.先用欧姆表粗测出常温下待测热敏电阻的阻值大约5Ω,热敏电阻和温度计插入带塞的保温杯中,杯内有一定量的冷水,其它备用的仪表和器具有:
热敏电阻是传感电路中常用的电子元件.现用伏安法测绘出热敏电阻分别在温度为t1=45℃和温度为t2=75℃时的伏安特性曲线,要求特性曲线尽可能完整.先用欧姆表粗测出常温下待测热敏电阻的阻值大约5Ω,热敏电阻和温度计插入带塞的保温杯中,杯内有一定量的冷水,其它备用的仪表和器具有: