题目内容
4．
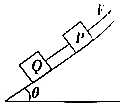如图所示，有材料相同的P、Q两物块通过轻绳相连，并在拉力F作用下沿斜面向上运动，轻绳与拉力F的方向均平行于斜面．当拉力F一定时，Q受到绳的拉力（ ）| A． | 与斜面倾角θ有关 | B． | 与摩擦因数有关 | ||
| C． | 与系统运动状态有关 | D． | 仅与两物块质量有关 |
分析 先对PQ整体受力分析，由牛顿第二定律列方程求出加速度a，然后隔离Q物体受力分析，由牛顿第二定律列方程即可求出Q受到绳的拉力．
解答 解：
设Q物体绳上的拉力大小F2，物体与斜面的动摩擦因数为μ，根据牛顿第二定律，对整体分析，有F-（mP+mQ）g（sinθ-μcosθ）=（mP+mQ）a，对Q分析，F2-mQg（sinθ-μcosθ）=mQa，联立以上两式可${F}_{2}=\frac{{m}_{Q}}{{m}_{P}+{m}_{Q}}F$，易知只有选项D正确．
故选：D
点评 本题考查了牛顿运动定律的综合应用中的连接体问题，解出此类题的关键是掌握整体法和隔离法的解题思想．
练习册系列答案
相关题目
15．两物体都做匀变速直线运动，在相同的时间间隔内，下列判断正确的是（ ）
| A． | 加速度越大的物体，速度改变越多 | |
| B． | 初速度越大的物体，位移一定越大 | |
| C． | 末速度越大的物体，位移一定越大 | |
| D． | 平均速度越大的物体，位移一定越大 |
12．
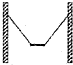如图，用两根长均为2d的轻绳将长为d，质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点，制成一简易秋千．某次维修时用另一块长为2d，质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉，绳子的悬挂点还在木板的两端点，木板静止时，F1表示木板所受合力大小，F2表示单根轻绳对未板拉力的大小，则维修后（ ）
如图，用两根长均为2d的轻绳将长为d，质量为m的均质木板悬挂在间距为3d竖直木桩上等高的两点，制成一简易秋千．某次维修时用另一块长为2d，质量为$\sqrt{\frac{6}{5}}m$木板将原木板换掉，绳子的悬挂点还在木板的两端点，木板静止时，F1表示木板所受合力大小，F2表示单根轻绳对未板拉力的大小，则维修后（ ）| A． | F1增大，F2增大 | B． | F1不变，F2增大 | C． | F1不变，F2减小 | D． | F1不变，F2不变 |
19．
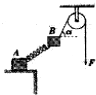如图，质量分别为M、m的两个木块A、B通过轻弹簧连接，木块A放在水平桌面上，木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态，绳与水平方向成α角．设最大静摩擦力等于滑动摩擦力，不计滑轮与绳间的摩擦．则可以求下列哪些量（ ）
如图，质量分别为M、m的两个木块A、B通过轻弹簧连接，木块A放在水平桌面上，木块B用轻绳通过定滑轮在力F的作用下整体恰好处于静止状态，绳与水平方向成α角．设最大静摩擦力等于滑动摩擦力，不计滑轮与绳间的摩擦．则可以求下列哪些量（ ）| A． | 木块A对桌面的压力 | B． | 弹簧与水平方向的夹角 | ||
| C． | 木块A与桌面之间的动摩擦因数 | D． | 弹簧的形变量 |
13．2009年7月16日，中国海军第三批护航编队16日已从浙江舟山某军港启航，于7月30日抵达亚丁湾、索马里海域，此次护航从舟山启航，经东海、台湾海峡、南海、马六甲海峡，穿越印度洋到达索马里海域执行护航任务，总航程为5千多海里，关于此次护航，下列说法正确的是（ ）
| A． | 当研究护航舰艇的运行轨迹时，不能将其看做质点 | |
| B． | “5千多海里”指的是护航舰艇的航行位移 | |
| C． | “5千多海里”指的是护航舰艇的航行路程 | |
| D． | 根据题中数据我们可以求得此次航行的平均速度 |
14．如图所示，直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置（x）-时间（t）图线．由图可知（ ）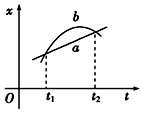
| A． | 在t1时刻，a、b两车相遇 | |
| B． | 在t2时刻，a、b两车运动方向相同 | |
| C． | 在t1到t2这段时间内，b车的速率先减小后增大 | |
| D． | 在t1到t2这段时间内，b车的速率一直比a车的大 |