题目内容
11．
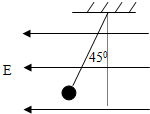质量为m的带电小球带电量为+q，用绝缘细线悬挂在水平向左的匀强电场中，平衡时绝缘细线与竖直方向成45°角，重力加速度为g．求电场强度的大小．
分析 对小球受力分析，受到重力、电场力和细线的拉力，根据电场力方向与场强方向的关系判断电性，根据共点力平衡条件和电场力F=qE列式求解场强E．
解答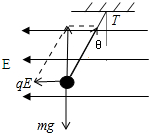 
解：对小球受力分析，受到重力、电场力和细线的拉力，结合平衡条件运用合成法，如图，
由几何知识得：mgtanθ=qE
解得：E=$\frac{mgtanθ}{q}$=$\frac{mg}{q}$
答：电场强度的大小为$\frac{mg}{q}$．
点评 本题关键是对小球受力分析，然后根据共点力平衡条件并通过合成法求解．
练习册系列答案
相关题目
如图所示，水平地面上的一辆小车在水平向右的拉力作用下，以速率v0向右做匀速直线运动，车内底面上紧靠左端面处有一光滑的小球，车的质量是小球质量的2倍，小球到车右端面的距离为L，车所受路面的摩擦阻力大小等于车对水平面压力的0.3倍．某时刻撤去水平拉力，经一段时间小球与车的右端面相撞，小球与车碰撞时间极短且碰撞后不再分离，已知重力加速度g=10m/s2．撤去拉力后，求：
6．如图所示的位移（x）-时间（t）图象和速度（v）-时间（t）图象中给出四条图线，甲、乙、丙、丁代表四辆车由同一地点向同一方向运动的情况，则下列说法正确的是（ ）
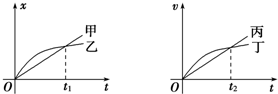
| A． | 0～t1时间内，甲车通过的路程等于乙车通过的路程 | |
| B． | 0～t2时间内，丙、丁两车在t2时刻相距最远 | |
| C． | 0～t2时间内，丙、丁两车的平均速度相等 | |
| D． | 甲车做直线运动，乙车做曲线运动 |
16．由静止开始做匀加速直线运动的汽车，第1s内通过0.4m位移，则正确的结论是（ ）
| A． | 第1s末的速度为0.8m/s | B． | 加速度为0.8m/s2 | ||
| C． | 第2S内通过位移为1.2 m | D． | 2S内通过位移为1.2 m |
3．物体的加速度为2m/s2，表示这个物体（ ）
| A． | 每秒运动2 m | |
| B． | 每经过1 s，其速度增大2 m/s | |
| C． | 每经过1 s，其速度变化量大小为2 m/s | |
| D． | 每经过1 s，其速度减小2 m/s |
20．
从倾角为θ的足够长斜面上的A点，先后将同一小球以不同的初速度水平向右抛出，不计空气阻力，下列关于小球的运动说法正确的是（ ）
从倾角为θ的足够长斜面上的A点，先后将同一小球以不同的初速度水平向右抛出，不计空气阻力，下列关于小球的运动说法正确的是（ ）| A． | 小球两次落到斜面上时的速度方向相同 | |
| B． | 小球从抛出到落到斜面上所用时间相等 | |
| C． | 小球两次落到斜面上时的动能与抛出的初速度成正比 | |
| D． | 小球两次从抛出到落到斜面上的过程中所发生的位移与初速度的二次方成正比 |
1．
如图所示，水平转台上的小物体A、B通过轻弹簧连接，并随转台一起匀速转动，A、B的质量分别为m、2m，A、B与转台的动摩擦因数均为μ，A、B离转台中心的距离分别为1.5r、r，已知弹簧的原长为1.5r，劲度系数为k，设最大静摩擦力等于滑动摩擦力，以下说法中正确的是（ ）
如图所示，水平转台上的小物体A、B通过轻弹簧连接，并随转台一起匀速转动，A、B的质量分别为m、2m，A、B与转台的动摩擦因数均为μ，A、B离转台中心的距离分别为1.5r、r，已知弹簧的原长为1.5r，劲度系数为k，设最大静摩擦力等于滑动摩擦力，以下说法中正确的是（ ）| A． | 当B受到的摩擦力为0时，转台转动的角速度为$\sqrt{\frac{k}{m}}$ | |
| B． | 当A受到的摩擦力为0时，转台转动的角速度为$\sqrt{\frac{k}{3m}}$ | |
| C． | 若转台转动的角速度为$\sqrt{\frac{k}{2m}+\frac{μg}{r}}$，则A不动，B刚好要滑动 | |
| D． | 转台转动的角速度为$\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$，则B不动，A刚好要滑动 |