题目内容
20. 从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )
从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )| A. | 小球两次落到斜面上时的速度方向相同 | |
| B. | 小球从抛出到落到斜面上所用时间相等 | |
| C. | 小球两次落到斜面上时的动能与抛出的初速度成正比 | |
| D. | 小球两次从抛出到落到斜面上的过程中所发生的位移与初速度的二次方成正比 |
分析 平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,抓住位移的方向相同,判断速度方向的关系.
根据竖直位移和水平位移的关系得出时间的表达式,从而比较运动的时间,结合速度时间公式求出竖直分速度,根据平行四边形定则求出速度的大小,从而得出动能的表达式,分析动能与初速度的关系.根据初速度和时间求出水平位移,从而得出位移的表达式,分析位移与初速度的关系.
解答 解:A、因为平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,小球落在斜面上位移的方向相同,则速度方向相同,故A正确.
B、根据$tanθ=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得:t=$\frac{2{v}_{0}tanθ}{g}$,由于初速度不同,则小球从抛出落到斜面上所用的时间不同,故B错误.
C、小球落在斜面上竖直分速度为:vy=gt=2v0tanθ,根据平行四边形定则知,落到斜面上的动能为:${E}_{k}=\frac{1}{2}m{v}^{2}$=$\frac{1}{2}m({{v}_{0}}^{2}+4{{v}_{0}}^{2}ta{n}^{2}θ)$,可知落在斜面上的动能与初速度的平方成正比,故C错误.
D、小球的水平位移为:x=${v}_{0}t=\frac{2{{v}_{0}}^{2}tanθ}{g}$,小球的位移为:$s=\frac{x}{cosθ}=\frac{2{{v}_{0}}^{2}tanθ}{gcosθ}$,可知小球落到斜面上发生的位移与初速度的二次方成正比,故D正确.
故选:AD.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度中等.

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )
一对平行金属板AB水平放置接在一个如图的、电压恒定的电源上,两板间有一带电的粒子P恰好静止在两板之间,现把两板的距离增大,将发生下列哪种现象( )| A. | 电路中有逆时针方向的电流同时P向下运动 | |
| B. | 电路中有顺时针方向的电流同时P向下运动 | |
| C. | 电路中有逆时针方向的电流同时P向上运动 | |
| D. | 电路中有顺时针方向的电流同时P向上运动 |
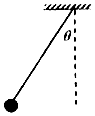 如图,长为L的细线悬挂一小球,小球的质量为m,使小球在竖直平面内运动,细线与竖直方向夹角为θ,则( )
如图,长为L的细线悬挂一小球,小球的质量为m,使小球在竖直平面内运动,细线与竖直方向夹角为θ,则( )| A. | θ最大时,细线对球的拉力小于mg | |
| B. | 只要θ≠0°,细线对球的拉力都小于mg | |
| C. | θ=0°时,细线对球的拉力等于mg | |
| D. | θ=0°时,细线对球的拉力小于mg |
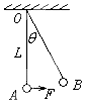 如图,质量为m的小球用长为L 的轻绳悬于O 点并处于静止状态.现用水平力F 将小球从A 点缓慢拉到B 点,OB 与竖直方向成θ角,则
如图,质量为m的小球用长为L 的轻绳悬于O 点并处于静止状态.现用水平力F 将小球从A 点缓慢拉到B 点,OB 与竖直方向成θ角,则(1)重力势能增加了多少?
(2)这过程克服重力所做的功是多少?
| A. | 向心加速度 | B. | 功 | C. | 线速度 | D. | 向心力 |
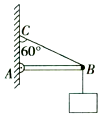 如图所示,一根质量不计的横梁的A端用铰链固定在墙壁上,B端用轻绳悬挂在墙壁上的C点,使得横梁保持水平状态,已知轻绳与竖直墙壁之间的夹角为60°,当用另一段轻绳在B点悬挂一个质量为m=6kg的物块时,横梁对B点的作用力大小应为(g取10m/s2)( )
如图所示,一根质量不计的横梁的A端用铰链固定在墙壁上,B端用轻绳悬挂在墙壁上的C点,使得横梁保持水平状态,已知轻绳与竖直墙壁之间的夹角为60°,当用另一段轻绳在B点悬挂一个质量为m=6kg的物块时,横梁对B点的作用力大小应为(g取10m/s2)( )| A. | 120N | B. | 30$\sqrt{3}$N | C. | 60$\sqrt{3}$N | D. | 60N |
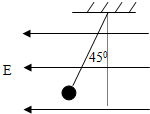 质量为m的带电小球带电量为+q,用绝缘细线悬挂在水平向左的匀强电场中,平衡时绝缘细线与竖直方向成45°角,重力加速度为g.求电场强度的大小.
质量为m的带电小球带电量为+q,用绝缘细线悬挂在水平向左的匀强电场中,平衡时绝缘细线与竖直方向成45°角,重力加速度为g.求电场强度的大小.