题目内容
19. 如图所示,水平地面上的一辆小车在水平向右的拉力作用下,以速率v0向右做匀速直线运动,车内底面上紧靠左端面处有一光滑的小球,车的质量是小球质量的2倍,小球到车右端面的距离为L,车所受路面的摩擦阻力大小等于车对水平面压力的0.3倍.某时刻撤去水平拉力,经一段时间小球与车的右端面相撞,小球与车碰撞时间极短且碰撞后不再分离,已知重力加速度g=10m/s2.撤去拉力后,求:
如图所示,水平地面上的一辆小车在水平向右的拉力作用下,以速率v0向右做匀速直线运动,车内底面上紧靠左端面处有一光滑的小球,车的质量是小球质量的2倍,小球到车右端面的距离为L,车所受路面的摩擦阻力大小等于车对水平面压力的0.3倍.某时刻撤去水平拉力,经一段时间小球与车的右端面相撞,小球与车碰撞时间极短且碰撞后不再分离,已知重力加速度g=10m/s2.撤去拉力后,求:(1)小车运动时的加速度大小;
(2)再经多长时间小球与车右端面相撞;
(3)小车向右运动的总路程.
分析 (1)由牛顿第二定律可以求出小车的加速度;
(2)应用匀变速直线运动的位移公式可以求出运动时间;
(3)应用动量守恒定律求出碰撞后的速度,然后应用匀变速直线运动的运动规律求出位移,再求出总路程.
解答 解:(1)设小球的质量为m,则车的质量为2m,所受路面阻力:f=0.3×3mg=9m.
根据牛顿第二定律:车与球相撞前,车的加速度大小${a_1}=\frac{f}{2m}=4.5m/{s^2}$
车与球相撞后,车的加速度大小:${a_2}=\frac{f}{3m}=3m/{s^2}$
(2)①若小球与车相撞时车还未停下,设相撞经历时间为t1,则
车的位移:${x_1}={v_0}{t_1}-\frac{1}{2}{a_1}t_1^2$,
小球的位移:x2=v0t1又 x2=L+x1
由以上各式解得:${t_1}=\frac{2}{3}\sqrt{L}$
②若小球与车相撞时车已停下,设相撞经历时间为t2,则车的位移为:${x'_1}=\frac{v_0^2}{{2{a_1}}}$,小球的位移为:x'2=v0t2又 x'2=L+x'1
由以上各式解得:${t_2}=\frac{L}{v_0}+\frac{{v_0^{\;}}}{9}$;
(3)①若小球与车相撞时车还未停下,则相撞前车的位移为:${x_1}={v_0}{t_1}-\frac{1}{2}{a_1}t_1^2=\frac{{2{v_0}}}{3}\sqrt{L}-L$,
相撞时车的速度:${v_1}={v_0}-{a_1}{t_1}={v_0}-3\sqrt{L}$,
相撞后共同速度为v,系统动量守恒,以碰撞前小车的速度方向为正方向,根据动量守恒定律得:2mv1+mv0=3mv,
解得:$v={v_0}-2\sqrt{L}$;
相撞后共同滑行位移:$x=\frac{v^2}{{2{a_2}}}=\frac{{{{({v_0}-2\sqrt{L})}^2}}}{6}$,
小车向右运动的总路程:${x_车}={x_1}+x=\frac{v_0^2-2L}{6}$;
②若小球与车相撞时车已停下,则相撞前车的位移为:${x'_1}=\frac{v_0^2}{{2{a_1}}}=\frac{v_0^2}{9}$
相撞后共同速度为v',以小球的初速度方向为正方向,根据动量守恒定律得:mv0=3mv',
解得:$v'=\frac{v_0}{3}$,
车相撞后位移:$x'=\frac{{{{v'}^2}}}{{2{a_2}}}=\frac{v_0^2}{54}$,
小车向右运动的总路程:${x'_车}={x'_1}+x'=\frac{7v_0^2}{54}$;
答:(1)小车运动时的加速度大小为4.5m/s2、3m/s2;
(2)再经过时间:$\frac{2}{3}$$\sqrt{L}$或$\frac{L}{{v}_{0}}$+$\frac{{v}_{0}}{9}$小球与车右端面相撞;
(3)小车向右运动的总路程为$\frac{{v}_{0}^{2}-2L}{6}$或$\frac{7{v}_{0}^{2}}{54}$.
点评 本题考查了求加速度、运动时间与路程问题,分析清楚物体的运动过程是解题的关键,应用牛顿第二定律、运动学公式与动量守恒定律可以解题;解题时注意讨论,否则会漏解.

 如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )
如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )| A. | 2.2V | B. | 1.9V | C. | 1.6V | D. | 1.4V |
| A. | 相等时间内的位移改变相等 | |
| B. | 速度改变始终相等 | |
| C. | 相等时间内的速度改变相等 | |
| D. | 瞬时速度的大小不断变化,方向一定不变 |
| A. | 电动势E的大小等于单位时间内非静电力所做的功 | |
| B. | 电动势E是由电源本身决定的,跟电源的体积和外电路均无关 | |
| C. | 电动势E的单位与电势、电势差的单位都是伏特,故三者本质上一样 | |
| D. | 电动势E是表征电源把其他形式的能转化为电能本领的物理量 |
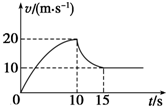 某跳伞运动员从悬停在高空的直升机上跳下,他从跳离飞机到落地的过程中在空中沿竖直方向运动的v-t图象如图所示,则下列关于他的运动情况分析正确的是( )
某跳伞运动员从悬停在高空的直升机上跳下,他从跳离飞机到落地的过程中在空中沿竖直方向运动的v-t图象如图所示,则下列关于他的运动情况分析正确的是( )| A. | 0~10 s加速度向下,10 s~15 s加速度向上 | |
| B. | 0~10 s、10 s~15 s内都在做加速度逐渐减小的变速运动 | |
| C. | 0~10 s内下落的距离大于100 m | |
| D. | 10 s~15 s内下落的距离大于75 m |
| A. | 向心加速度 | B. | 功 | C. | 线速度 | D. | 向心力 |
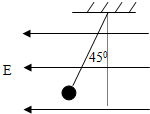 质量为m的带电小球带电量为+q,用绝缘细线悬挂在水平向左的匀强电场中,平衡时绝缘细线与竖直方向成45°角,重力加速度为g.求电场强度的大小.
质量为m的带电小球带电量为+q,用绝缘细线悬挂在水平向左的匀强电场中,平衡时绝缘细线与竖直方向成45°角,重力加速度为g.求电场强度的大小.