题目内容
11.一台发电机最大输出功率为4000kW,电压为4000V,经变压器T1升压后向远方输电.输电线路总电阻R=1kΩ.到目的地经变压器T2降压,负载为多个正常发光的灯泡(220V、60W).若在输电线路上消耗的功率为发电机输出功率的10%,变压器T1和T2的损耗可忽略,则T1和T2的变压比分别为1:50和9000:11;此发电机最多能使$6×1{0}_{\;}^{4}$盏灯泡(220V、60W)正常发光.分析 根据电压与匝数成正比,电流与匝数成反比,可以求得降压变压器的电流和输电线上的电流的大小,从而可以求得输电线和用电器消耗的功率的大小.由于降压变压器的负载能正常工作,则可算出降压变压器的原线圈的匝数之比,同时能确定接入多少个灯泡才正常发光.
解答 解:由P=UI可得升压变压器输入电流为:
${I}_{1}^{\;}$=$\frac{P}{U}=\frac{4000×1{0}_{\;}^{3}}{4×1{0}_{\;}^{3}}=1×1{0}_{\;}^{3}A$
由P损=I2R得升压变压器的输出电流为:
${I}_{2}^{\;}=\sqrt{\frac{{P}_{损}^{\;}}{R}}=\sqrt{\frac{10%×4000×1{0}_{\;}^{3}}{1000}}=20A$
由$\frac{{I}_{1}^{\;}}{{I}_{2}^{\;}}=\frac{{n}_{2}^{\;}}{{n}_{1}^{\;}}$得${T}_{1}^{\;}$的变压比为:
$\frac{{n}_{1}^{\;}}{{n}_{2}^{\;}}=\frac{{I}_{2}^{\;}}{{I}_{1}^{\;}}=\frac{20}{1×1{0}_{\;}^{3}}=\frac{1}{50}$
根据$\frac{{n}_{1}^{\;}}{{n}_{2}^{\;}}=\frac{{U}_{1}^{\;}}{{U}_{2}^{\;}}$得升压变压器的输出电压为:
${U}_{2}^{\;}=\frac{{n}_{2}^{\;}}{{n}_{1}^{\;}}{U}_{1}^{\;}=2×1{0}_{\;}^{5}V$
输电线上的电压损失为:
U损=I2R=20×1000V=2×104V
降压变压器的输入电压${U}_{3}^{\;}={U}_{2}^{\;}-{I}_{2}^{\;}R=1.8×1{0}_{\;}^{5}V$
用户得到的电压即为降压变压器的输出电压U4=220V
降压变压器${T}_{2}^{\;}$的匝数比$\frac{{n}_{3}^{\;}}{{n}_{4}^{\;}}=\frac{{U}_{3}^{\;}}{{U}_{4}^{\;}}=\frac{1.8×1{0}_{\;}^{5}}{220}=\frac{9000}{11}$
用户得到的功率P3=P2-10%P2=0.9×4000KW=3600KW
可供灯泡正常发光的盏数n=$\frac{{P}_{3}^{\;}}{{P}_{灯}^{\;}}=\frac{3600×1{0}_{\;}^{3}}{60}=6×1{0}_{\;}^{4}$盏
故答案为:1:50、9000:11、$6×1{0}_{\;}^{4}$
点评 本题考查远距离输电中的能量损失及功率公式的应用,要注意功率公式中P=UI中的电压U应为输电电压,不是发电机的输出电压.本题突破点是由输电线上的损失功率,从而算出电线上的电流

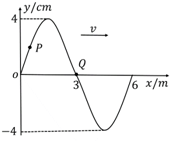 一简谐横波沿x轴正方向传播,在t=0时刻的波形如图所示.已知介质中质点P的振动周期为2s,此时P点的纵坐标为(0.5m,2cm),Q点的坐标为(3m,0cm).则以下说法正确的是( )
一简谐横波沿x轴正方向传播,在t=0时刻的波形如图所示.已知介质中质点P的振动周期为2s,此时P点的纵坐标为(0.5m,2cm),Q点的坐标为(3m,0cm).则以下说法正确的是( )| A. | 当t=$\frac{1}{2}$s时,P点在波峰 | B. | 当t=$\frac{11}{3}$s时,P点在波峰 | ||
| C. | 当t=$\frac{13}{6}$s时,P点在平衡位置 | D. | 当t=$\frac{3}{2}$s时,P点在波谷 | ||
| E. | 这列波的波速为3m/s |

| A. | 3 m/s | B. | 5 m/s | C. | 1 m/s | D. | 10 m/s |
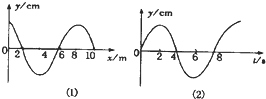 一列简谐横波沿X轴正方向传播,图1是t=0时刻的波形图,图2是波中某振动质点位移随时间变化的振动图象(两图用同一时间起点),则图2可能是图1中哪个质点的振动图线( )
一列简谐横波沿X轴正方向传播,图1是t=0时刻的波形图,图2是波中某振动质点位移随时间变化的振动图象(两图用同一时间起点),则图2可能是图1中哪个质点的振动图线( )| A. | x=0处的质点 | B. | x=2m处的质点 | C. | x=4m处的质点 | D. | x=6m处的质点 |
| A. | 0.10 s | B. | 0.13 s | C. | 0.20 s | D. | 0.50 s |
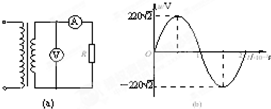 如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )
如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )| A. | 电压表的示数为110V | B. | 原线圈输入功率为440W | ||
| C. | 通过电阻R的电流的频率为25Hz | D. | 电流表的示数为2A |
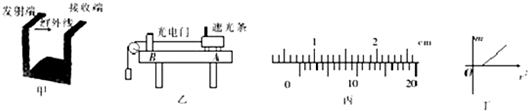
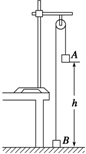 如图为验证机械能守恒定律的实验装置示意图.两个质量各为mA和mB(mA>mB)的小物块A和B分别系在一条跨过定滑轮的软绳两端,用手拉住物块B,使它与地面接触,用米尺测量物块A的底部到地面的高度h.释放物块B,同时用秒表开始计时,当物块A碰到地面时,停止计时,记下物块A下落的时间t,当地的重力加速度为g.
如图为验证机械能守恒定律的实验装置示意图.两个质量各为mA和mB(mA>mB)的小物块A和B分别系在一条跨过定滑轮的软绳两端,用手拉住物块B,使它与地面接触,用米尺测量物块A的底部到地面的高度h.释放物块B,同时用秒表开始计时,当物块A碰到地面时,停止计时,记下物块A下落的时间t,当地的重力加速度为g.