题目内容
9.如图1所示,用一根不可伸长的轻质细线将小球悬挂在天花板上的O点,现将小球拉离平衡位置,使细线与竖直方向成一夹角(该夹角小于5°)后由静止释放.小球的大小和受到的空气阻力忽略不计.(1)证明小球的运动是简谐运动;
(2)由传感器测得小球偏离平衡位置的位移随时间变化的规律如图2所示,求小球运动过程中的最大速度值.

分析 (1)简谐运动的特征是F=-kx.单摆的回复力是重力沿圆弧切线方向的分力,在摆角θ<5°,sinθ≈$\frac{x}{L}$,得到单摆的回复力与位移的关系式,即可证明.
(2)由图2可得到摆球的振幅A=0.08m,周期T=2s.根据单摆的周期公式救出摆长,由机械能守恒得最大速度.
解答 解:(1)设小球偏角为θ时离开平衡位置的位移为x,摆长为L,θ<5°,则:
x=θL
sinθ≈θ
小球受到的回复力大小:F=mgsinθ
联立解得:$F=\frac{mg}{L}x$
且因F与x方向相反,故有F=-$\frac{mg}{L}$x,则小球做简谐运动.
ⅱ.由图2可知摆球的振幅A=0.08m,周期T=2s
以摆球为研究对象:由周期公式:$T=2π\sqrt{\frac{L}{g}}$
由机械能守恒:$mgL(1-cosθ)=\frac{1}{2}mv_{max}^2$
由三角函数知识:$1-cosθ=2{sin^2}\frac{θ}{2}≈\frac{θ^2}{2}$
由圆的知识:$θ=\frac{A}{L}$
联立解得:$v_{max}^{\;}=0.08πm/s$
答:
(1)证明见上.
(2)小球运动过程中的最大速度值为0.08πm/s.
点评 解决本题的关键要关键掌握简谐运动的特征,围绕这个特征分析单摆的回复力与位移的关系,从而进行证明.

练习册系列答案
相关题目
19. 如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
 如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )| A. | 交变电压的有效值为$\sqrt{2}V$ | |
| B. | 0~4s内交变电压的平均值为$\frac{\sqrt{2}}{2}V$ | |
| C. | 1s末线框平面平行于磁场,通过线框的磁通量变化最快 | |
| D. | 2s时通过线框的磁通量为零 |
17. 如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
 如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )| A. | 小球A的合力小于小球B的合力 | |
| B. | 小球A与框架间可能没有摩擦力 | |
| C. | 小球B与框架间可能没有摩擦力 | |
| D. | 圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大 |
14. 如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
 如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )| A. | b球一定先落在斜面上 | |
| B. | a球可能垂直落在半圆轨道上 | |
| C. | a、b两球可能同时落在半圆轨道和斜面上 | |
| D. | a、b两球不可能同时落在半圆轨道和斜面上 |
18. 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )
 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )| A. | 小球运动到最高点时所受的向心力不一定等于重力 | |
| B. | 小球在最高点时绳子的拉力不可能为零 | |
| C. | 小球运动到最高点的速率一定大于$\sqrt{gL}$ | |
| D. | 小球经过最低点时绳子的拉力一定大于小球重力 |
19. 如图为测电源电动势和内电阻的实验中得到的图线,图中U为路端电压,I为流过电源的电流,图线上P点对应的状态,其电源的效率为( )
如图为测电源电动势和内电阻的实验中得到的图线,图中U为路端电压,I为流过电源的电流,图线上P点对应的状态,其电源的效率为( )
 如图为测电源电动势和内电阻的实验中得到的图线,图中U为路端电压,I为流过电源的电流,图线上P点对应的状态,其电源的效率为( )
如图为测电源电动势和内电阻的实验中得到的图线,图中U为路端电压,I为流过电源的电流,图线上P点对应的状态,其电源的效率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
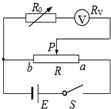 某同学采用“半偏法”测量一个量程为3V的电压表的内阻.
某同学采用“半偏法”测量一个量程为3V的电压表的内阻. 17世纪,英国天文学家哈雷跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定的时间飞临地球,后来哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星围绕太阳公转的轨道是一个非常扁的椭圆,如图所示.从公元前240年起,哈雷彗星每次回归,中国均有记录.它最近一次回归的时间是1986年.从公元前240年至今,我国关于哈雷彗星回归记录的次数,最合理的是( )
17世纪,英国天文学家哈雷跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定的时间飞临地球,后来哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星围绕太阳公转的轨道是一个非常扁的椭圆,如图所示.从公元前240年起,哈雷彗星每次回归,中国均有记录.它最近一次回归的时间是1986年.从公元前240年至今,我国关于哈雷彗星回归记录的次数,最合理的是( ) 如图所示,某种透明材料做成的三棱镜,其横截面是边长为a的等边三角形,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB及AC面上,结果所有从AB、AC面入射的光线进入后恰好全部直接到达BC面.求:
如图所示,某种透明材料做成的三棱镜,其横截面是边长为a的等边三角形,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB及AC面上,结果所有从AB、AC面入射的光线进入后恰好全部直接到达BC面.求: