题目内容
1. 如图所示,某种透明材料做成的三棱镜,其横截面是边长为a的等边三角形,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB及AC面上,结果所有从AB、AC面入射的光线进入后恰好全部直接到达BC面.求:
如图所示,某种透明材料做成的三棱镜,其横截面是边长为a的等边三角形,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB及AC面上,结果所有从AB、AC面入射的光线进入后恰好全部直接到达BC面.求:(i)该材料对此平行光束的折射率;
(ii)这些直接到达BC面的光线从BC面折射而出后,如果照射到一块平行于BC面的屏上形成光斑,则当屏到BC面的距离d满足什么条件时,此光斑分为两条?
分析 (i)先据题意知从AB、AC面入射的光线进入后恰好全部直接到达BC面,说明从AB面进入三棱镜的折射光线与AC平行,画出光路图,根据对称性和几何关系得到入射角和折射角,即可求得折射率.
(ii)画出光路图,如图O为BC中点,在B点附近折射的光线从BC射出后与直线AO交于D,可看出只要光屏放得比D点远,则光斑会分成两块,由几何知识求解.
解答  解:(i)由于对称性,我们考虑从AB面入射的光线,这些光线在棱镜中是平行于AC面的,由对称性和几何知识可得,光线进入AB面时的入射角α和折射角β分别为:
解:(i)由于对称性,我们考虑从AB面入射的光线,这些光线在棱镜中是平行于AC面的,由对称性和几何知识可得,光线进入AB面时的入射角α和折射角β分别为:
α=60°,β=30°
则材料的折射率为 n=$\frac{sinα}{sinβ}$=$\sqrt{3}$
(ii)如图O为BC中点,紧靠B点从BC面射出的光线与直线AO交于D,由图可知:当光屏放在D点右侧时,根据对称性,光屏上形成两条光斑.
由几何关系有 OD=$\frac{a}{2}$tanα=$\frac{\sqrt{3}}{6}$a
所以当光屏到BC距离d超过$\frac{\sqrt{3}}{6}$a时,光斑分为两条.
答:
(i)该材料对此平行光束的折射率为$\sqrt{3}$;
(ii)当光屏到BC距离d超过$\frac{\sqrt{3}}{6}$a时,光斑分为两条.
点评 本题是几何光学问题,作出光路图是解题的关键之处,再运用几何知识求出入射角和折射角,即能解决此类问题.

练习册系列答案
相关题目
11.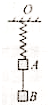 如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
 如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )| A. | mA=mB | B. | mA>mB | C. | mA<mB | D. | 无法确定 |
12. 如图所示为小型旋转电枢式交流发电机,电阻r=1Ω的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )
如图所示为小型旋转电枢式交流发电机,电阻r=1Ω的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )
 如图所示为小型旋转电枢式交流发电机,电阻r=1Ω的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )
如图所示为小型旋转电枢式交流发电机,电阻r=1Ω的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )| A. | 电阻R1消耗的功率为$\frac{2}{3}$W | |
| B. | 0.02 s时滑动变阻器R两端的电压瞬时值为零 | |
| C. | 线圈产生的电动势e随时间t变化的规律是e=6$\sqrt{2}$sin100πt(V) | |
| D. | 线圈从开始计时到$\frac{1}{200}$s的过程中,通过R1的电荷量为$\frac{\sqrt{2}}{200π}$C |
16. 如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=10:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和电流表对电路的影响可忽略不计,定值电阻R0=10Ω,可变电阻R的阻值范围为0~10Ω,则( )
如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=10:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和电流表对电路的影响可忽略不计,定值电阻R0=10Ω,可变电阻R的阻值范围为0~10Ω,则( )
 如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=10:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和电流表对电路的影响可忽略不计,定值电阻R0=10Ω,可变电阻R的阻值范围为0~10Ω,则( )
如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=10:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和电流表对电路的影响可忽略不计,定值电阻R0=10Ω,可变电阻R的阻值范围为0~10Ω,则( )| A. | 副线圈中交变电流的频率为100Hz | |
| B. | t=0.02s时,电压表的示数为0 | |
| C. | 调节可变电阻R的阻值时,电流表示数的变化范围为1.1A~2.2A | |
| D. | 当可变电阻阻值为10Ω时,变压器的输入电功率为24.2W |
6. 一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
 一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )| A. | E1>E2,I1沿逆时针方向,I2沿顺时针方向 | |
| B. | E1<E2,I1沿逆时针方向,I2沿顺时针方向 | |
| C. | E1<E2,I2沿顺时针方向,I3沿逆时针方向 | |
| D. | E2=E3,I2沿顺时针方向,I3沿顺时针方向 |
13.以下说法中符合史实的是( )
| A. | 哥白尼通过观察行星的运动,提出了日心说,认为行星以椭圆轨道绕太阳运行 | |
| B. | 开普勒通过对行星运动规律的研究,总结出了万有引力定律 | |
| C. | 卡文迪许利用扭秤装置测出了万有引力常量的数值 | |
| D. | 牛顿将斜面实验的结论合理外推,间接证明了自由落体运动是匀变速直线运动 |






