题目内容
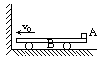
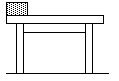
如图所示,光滑水平面上有一辆质量为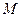 =1kg的小车,小车的上表面有一个质量为
=1kg的小车,小车的上表面有一个质量为 =0.9kg的滑块,在滑块与小车的挡板间用轻弹簧相连接,滑块与小车上表面间的动摩擦因数为μ=0.2,整个系统一起以
=0.9kg的滑块,在滑块与小车的挡板间用轻弹簧相连接,滑块与小车上表面间的动摩擦因数为μ=0.2,整个系统一起以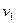 =10m/s的速度向右做匀速直线运动,此时弹簧长度恰好为原长.现在用一质量为
=10m/s的速度向右做匀速直线运动,此时弹簧长度恰好为原长.现在用一质量为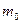 =0.1kg的子弹,以
=0.1kg的子弹,以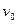 =50m./s的速度向左射入滑块且不穿出,所用时间极短,当弹簧压缩到最短时,弹簧被锁定,测得此时弹簧的压缩量为
=50m./s的速度向左射入滑块且不穿出,所用时间极短,当弹簧压缩到最短时,弹簧被锁定,测得此时弹簧的压缩量为 =0.50m, g =10m/s2.求:
=0.50m, g =10m/s2.求:

(1)子弹射入滑块后的瞬间,子弹与滑块共同速度的大小和方向;
(2)弹簧压缩到最短时,小车的速度和弹簧的弹性势能的大小.
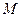 =1kg的小车,小车的上表面有一个质量为
=1kg的小车,小车的上表面有一个质量为 =0.9kg的滑块,在滑块与小车的挡板间用轻弹簧相连接,滑块与小车上表面间的动摩擦因数为μ=0.2,整个系统一起以
=0.9kg的滑块,在滑块与小车的挡板间用轻弹簧相连接,滑块与小车上表面间的动摩擦因数为μ=0.2,整个系统一起以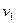 =10m/s的速度向右做匀速直线运动,此时弹簧长度恰好为原长.现在用一质量为
=10m/s的速度向右做匀速直线运动,此时弹簧长度恰好为原长.现在用一质量为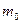 =0.1kg的子弹,以
=0.1kg的子弹,以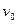 =50m./s的速度向左射入滑块且不穿出,所用时间极短,当弹簧压缩到最短时,弹簧被锁定,测得此时弹簧的压缩量为
=50m./s的速度向左射入滑块且不穿出,所用时间极短,当弹簧压缩到最短时,弹簧被锁定,测得此时弹簧的压缩量为 =0.50m, g =10m/s2.求:
=0.50m, g =10m/s2.求:
(1)子弹射入滑块后的瞬间,子弹与滑块共同速度的大小和方向;
(2)弹簧压缩到最短时,小车的速度和弹簧的弹性势能的大小.
(1)v2= 4m/s,方向水平向右; (2)8 J
⑴ 子弹射入滑块后的共同速度大为v2,设向右为正方向,对子弹与滑块组成的系统应用动量守恒定律得
mv1—mv0= (m+m0) v2 (4分)
v2= 4m/s,方向水平向右; (2分)
⑵子弹,滑块与小车,三者的共同速度为v3,当三者达到共同速度时弹簧压缩量最大,弹性势能最大.由动量守恒定律得
Mv1+(m+m0)v2 = (M+m+m0)v3 (3分)
v3=7m/s,方向水平向右. (2分)
设最大弹性势能为防Epmax对三个物体组成的系统应用能量守恒定律
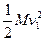 +
+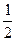 (m+m0)v22 =" " EPmax +
(m+m0)v22 =" " EPmax + 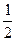 (M+m+m0) v32+μ(m+m0)gd (3分)
(M+m+m0) v32+μ(m+m0)gd (3分)EPmax=" 8" J (2分)

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
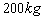 ,载有质量为
,载有质量为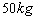 的人,静止在空中离地
的人,静止在空中离地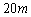 高处,气球下悬一根质量可忽略不计的绳子,一人想从气球上沿绳慢慢滑到地面,为了安全到达地面,这根绳长至少应为(不计人的高度)多长?
高处,气球下悬一根质量可忽略不计的绳子,一人想从气球上沿绳慢慢滑到地面,为了安全到达地面,这根绳长至少应为(不计人的高度)多长? 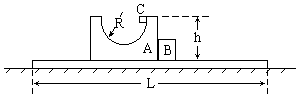

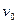 击中木块A并留在其中,子弹打入木块的过程持续时间极短,可
击中木块A并留在其中,子弹打入木块的过程持续时间极短,可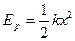 .如果此后运动过程中弹簧始终处于弹性限度内,且A、B不会发生直接碰触。试求:
.如果此后运动过程中弹簧始终处于弹性限度内,且A、B不会发生直接碰触。试求: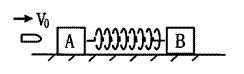
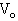 与竖直墙壁相撞.若碰撞时间极短且无能量损失,撞后A恰好未从B上落下来,A与B间的动摩擦因数为μ.
与竖直墙壁相撞.若碰撞时间极短且无能量损失,撞后A恰好未从B上落下来,A与B间的动摩擦因数为μ.