题目内容
如图所示，两只质量均为120kg的小船静止在水面上，相距10m，并用钢绳连接。一个质量为60kg的人在船头以恒力F拉绳，不计水的阻力，求：
（1）当两船相遇时，两船各行进了多少米？
（2）当两船相遇不相碰的瞬间，为了避免碰撞，人从甲船跳向乙船需要对地的最小水平速度为6m/s，计算原来人拉绳的恒力F。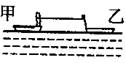
（1）当两船相遇时，两船各行进了多少米？
（2）当两船相遇不相碰的瞬间，为了避免碰撞，人从甲船跳向乙船需要对地的最小水平速度为6m/s，计算原来人拉绳的恒力F。
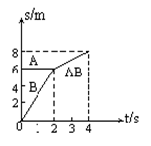
（1）s甲=4m，s乙=6m
（2）F=90N
（2）F=90N
（1）由动量守恒定律，得(m甲+m人)v甲=m乙v乙 有(m甲+m人)s甲=m乙s乙
s甲+s乙="10m " 得，s甲="4m " s乙=6m
（2）为了避免碰撞，人跳到乙船后系统至少要静止。设人在起跳前瞬间甲船和人的速度为v1，乙船速度为v2，对甲船和人组成的系统由动量守恒得，(m甲+m人)v1=m人×6m/s
得v1="2m/s " 由动能定理得，Fs甲=(m甲+m人)v12/2 解得F=90N。
s甲+s乙="10m " 得，s甲="4m " s乙=6m
（2）为了避免碰撞，人跳到乙船后系统至少要静止。设人在起跳前瞬间甲船和人的速度为v1，乙船速度为v2，对甲船和人组成的系统由动量守恒得，(m甲+m人)v1=m人×6m/s
得v1="2m/s " 由动能定理得，Fs甲=(m甲+m人)v12/2 解得F=90N。
练习册系列答案
相关题目
、
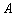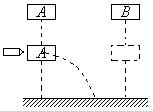
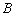两木块从同一高度自由下落，至某一位置时，A被水平飞来的子弹很快击中（子弹未穿出），则
，
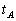的关系是：（ ）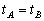
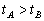
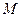=1kg的小车，小车的上表面有一个质量为
=0.9kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ=0.2，整个系统一起以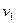
=10m/s的速度向右做匀速直线运动，此时弹簧长度恰好为原长．现在用一质量为
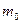=0.1kg的子弹，以
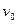=50m./s的速度向左射入滑块且不穿出，所用时间极短，当弹簧压缩到最短时，弹簧被锁定，测得此时弹簧的压缩量为
=0.50m， g =10m/s2．求：
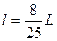
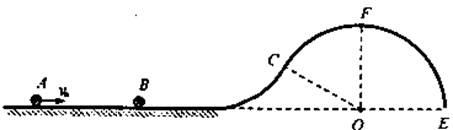
=15kg，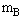
=5kg，车长L=4m．B位于A的左端，与A一起以
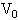=4m/s的速度向右运动．右面有一固定的墙壁，A与墙壁碰撞时间极短，碰撞后以原速率向左运动，而B则仍向右运动．由于A、B间有摩擦力，最后B恰停在A的右端而没有掉下来．求AB间的动摩擦因数．(取g=10m/
)
