题目内容
10.一个5kg的物体在半径为4m的圆周上以4m/s的速度做匀速圆周运动,向心加速度是多大?所需向心力是多大?分析 已知物体做圆周运动的线速度v=4m/s,半径r=4m,物体的质量为m=5kg,根据公式${a}_{n}=\frac{{v}^{2}}{r}$求解向心加速度,由公式${F}_{n}=m\frac{{v}^{2}}{r}$求解向心力
解答 解:由题,物体做圆周运动的线速度v=4m/s,半径r=4m,则物体的向心加速度为
${a}_{n}=\frac{{v}^{2}}{r}=\frac{16}{4}$m/s2=4m/s2
物体所需的向心力${F}_{n}=m\frac{{v}^{2}}{r}=5×4=20N$
答:向心加速度是4m/s2,所需向心力是20N.
点评 向心力公式形式有下列几种:${a}_{n}=\frac{{v}^{2}}{r}$=ω2r=$\frac{4{π}^{2}}{{T}^{2}}$r=vω,要根据不同的条件选择不同形式的公式,难度不大,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.位于赤道面上的一颗人造地球卫星绕地球运行,傍晚在赤道上的某人发现卫星位于自己的正上方相对地面运动,第二天傍晚同一时刻又发现此卫星出现在自己的正上方,已知地球自传角速度为ω0,地表处重力加速度为g0,地球半径为R0,则对此卫星下列说法正确的是( )
| A. | 一定是同步卫星 | |
| B. | 可能是同步卫星 | |
| C. | 此卫星距地面的高度可能是$\root{3}{\frac{{g}_{0}{R}_{0}^{2}}{4{ω}_{0}^{2}}}$-R0 | |
| D. | 此卫星距地面的高度可能是$\root{3}{\frac{{g}_{0}{R}_{0}^{2}}{{ω}_{0}^{2}}}$-R0 |
1. 如图所示,粗糙水平圆盘上,M、N两物块叠放在一起,随圆盘一起绕过圆盘圆心的中心轴做匀速圆周运动.用μ1、μ2分别表示圆盘对N、N对M的动摩擦因数,现缓慢增大圆盘转动的角速度.已知最大动摩擦力等于滑动摩擦力.下列说法正确的是( )
如图所示,粗糙水平圆盘上,M、N两物块叠放在一起,随圆盘一起绕过圆盘圆心的中心轴做匀速圆周运动.用μ1、μ2分别表示圆盘对N、N对M的动摩擦因数,现缓慢增大圆盘转动的角速度.已知最大动摩擦力等于滑动摩擦力.下列说法正确的是( )
 如图所示,粗糙水平圆盘上,M、N两物块叠放在一起,随圆盘一起绕过圆盘圆心的中心轴做匀速圆周运动.用μ1、μ2分别表示圆盘对N、N对M的动摩擦因数,现缓慢增大圆盘转动的角速度.已知最大动摩擦力等于滑动摩擦力.下列说法正确的是( )
如图所示,粗糙水平圆盘上,M、N两物块叠放在一起,随圆盘一起绕过圆盘圆心的中心轴做匀速圆周运动.用μ1、μ2分别表示圆盘对N、N对M的动摩擦因数,现缓慢增大圆盘转动的角速度.已知最大动摩擦力等于滑动摩擦力.下列说法正确的是( )| A. | 若μ1>μ2,则M将先于N远离圆盘圆心 | |
| B. | 若μ1>μ2,则M与N将一起同时开始远离圆盘圆心 | |
| C. | 若μ1<μ2,则M将先于N远离圆盘圆心 | |
| D. | 若μ1<μ2,则M与N将一起同时开始远离圆盘圆心 |
15. 如图所示,质量均为m的木块A和B,用劲度系数为k的轻质弹簧连接,最初系统静止.现用大小F=2mg、方向竖直向上的恒力拉A直到B,刚好离开地面,则在此过程中( )
如图所示,质量均为m的木块A和B,用劲度系数为k的轻质弹簧连接,最初系统静止.现用大小F=2mg、方向竖直向上的恒力拉A直到B,刚好离开地面,则在此过程中( )
 如图所示,质量均为m的木块A和B,用劲度系数为k的轻质弹簧连接,最初系统静止.现用大小F=2mg、方向竖直向上的恒力拉A直到B,刚好离开地面,则在此过程中( )
如图所示,质量均为m的木块A和B,用劲度系数为k的轻质弹簧连接,最初系统静止.现用大小F=2mg、方向竖直向上的恒力拉A直到B,刚好离开地面,则在此过程中( )| A. | A上升的初始加速度大小为2g | |
| B. | 弹簧对A和对B的弹力是一对作用力与反作用力 | |
| C. | A上升的最大高度为$\frac{mg}{k}$ | |
| D. | A上升的速度先增大后减少 |
19. 如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
 如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )| A. | 交变电压的有效值为$\sqrt{2}V$ | |
| B. | 0~4s内交变电压的平均值为$\frac{\sqrt{2}}{2}V$ | |
| C. | 1s末线框平面平行于磁场,通过线框的磁通量变化最快 | |
| D. | 2s时通过线框的磁通量为零 |

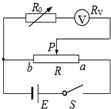 某同学采用“半偏法”测量一个量程为3V的电压表的内阻.
某同学采用“半偏法”测量一个量程为3V的电压表的内阻.