题目内容
8. 如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求:
如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求:(1)物块经过A点时的速度大小;
(2)欲使物块经过B点时对圆弧面的压力恰好为0,则恒力F的大小应为多少?
分析 (1)以质点为研究对象,分析清楚质点的受力和运动情况,据动能定理即可求解.
(2)据在最高点的压力恰好为零,据牛顿第二定律列式,再利用机械能守恒列式求解即可.
解答 解:(1)由动能定理得 $\frac{FL}{2}$-μmgL=$\frac{1}{2}$mvA2
解得:vA=$\sqrt{\frac{FL}{m}-2μgL}$
(2)物块在B点是圆周运动的一个状态,
由于压力为零,由牛顿第二定律得:mg=$\frac{m{v}_{B}^{2}}{R}$
物块从A运动到B的过程机械能守恒:$\frac{1}{2}$mvA2=mgh+$\frac{1}{2}m{v}_{B}^{2}$
联立解得:F=2μmg+$\frac{2mgh}{L}$+$\frac{mgR}{L}$
答:(1)物块经过A点时的速度大小$\sqrt{\frac{FL}{m}-2μgL}$;
(2)欲使物块经过B点时对圆弧面的压力恰好为0,则恒力F的大小应2μmg+$\frac{2mgh}{L}$+$\frac{mgR}{L}$.
点评 本题看图感觉难度较大,如弄清质点的运动情况和遵循的规律,此题就可迎刃而解,善于利用临界状态分析,灵活应用动能定理和机械能守恒定律是关键.

练习册系列答案
相关题目
13. 如图所示,一形状为等边三角形的绝缘支架处在匀强电场中,支架可绕顶点A转动,B,C两个顶点分别固定着带电量为+q,-q的两个带电小球,图示位置处的电势分别为φA=φB=0,φC=φ,现让支架以A点为轴在纸面内顺时针转过30°,不计两带电小球对电场的影响,系统的电势能为( )
如图所示,一形状为等边三角形的绝缘支架处在匀强电场中,支架可绕顶点A转动,B,C两个顶点分别固定着带电量为+q,-q的两个带电小球,图示位置处的电势分别为φA=φB=0,φC=φ,现让支架以A点为轴在纸面内顺时针转过30°,不计两带电小球对电场的影响,系统的电势能为( )
 如图所示,一形状为等边三角形的绝缘支架处在匀强电场中,支架可绕顶点A转动,B,C两个顶点分别固定着带电量为+q,-q的两个带电小球,图示位置处的电势分别为φA=φB=0,φC=φ,现让支架以A点为轴在纸面内顺时针转过30°,不计两带电小球对电场的影响,系统的电势能为( )
如图所示,一形状为等边三角形的绝缘支架处在匀强电场中,支架可绕顶点A转动,B,C两个顶点分别固定着带电量为+q,-q的两个带电小球,图示位置处的电势分别为φA=φB=0,φC=φ,现让支架以A点为轴在纸面内顺时针转过30°,不计两带电小球对电场的影响,系统的电势能为( )| A. | -$\frac{2\sqrt{3}}{3}$qφ | B. | -$\frac{\sqrt{3}}{3}$qφ | C. | -qφ | D. | qφ |
19. 磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )
磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )
 磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )
磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )| A. | $\sqrt{\frac{2μF}{S}}$ | B. | $\sqrt{\frac{2SF}{μ}}$ | C. | $\sqrt{\frac{μF}{S}}$ | D. | $\sqrt{\frac{SF}{μ}}$ |
3.甲和乙是绕某天体做匀速圆周运动的两颗卫星,甲的半径为r1,周期为T1,乙的周期为T2,且T1>T2,下列说法正确的是( )
| A. | 甲的线速度较大 | |
| B. | 甲的向心加速度较大 | |
| C. | 利用所给条件可以求出天体的质量 | |
| D. | 利用所给条件可以求出天体的平均密度 |
13.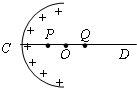 如图所示,电荷q均匀分布在半球面上,球面的半径为R,CD为通过半球顶点C与球心O的轴线,P、Q为CD轴上在O点两侧且离O点距离相等的二点.已知带电量为Q的均匀带电球壳,其内部电场强度处处为零,电势处处相等.以无穷远为零电势点,则下列判断正确的是( )
如图所示,电荷q均匀分布在半球面上,球面的半径为R,CD为通过半球顶点C与球心O的轴线,P、Q为CD轴上在O点两侧且离O点距离相等的二点.已知带电量为Q的均匀带电球壳,其内部电场强度处处为零,电势处处相等.以无穷远为零电势点,则下列判断正确的是( )
 如图所示,电荷q均匀分布在半球面上,球面的半径为R,CD为通过半球顶点C与球心O的轴线,P、Q为CD轴上在O点两侧且离O点距离相等的二点.已知带电量为Q的均匀带电球壳,其内部电场强度处处为零,电势处处相等.以无穷远为零电势点,则下列判断正确的是( )
如图所示,电荷q均匀分布在半球面上,球面的半径为R,CD为通过半球顶点C与球心O的轴线,P、Q为CD轴上在O点两侧且离O点距离相等的二点.已知带电量为Q的均匀带电球壳,其内部电场强度处处为零,电势处处相等.以无穷远为零电势点,则下列判断正确的是( )| A. | P点与Q点的电场强度大小相等 | B. | P点与Q点的电场强度大小不等 | ||
| C. | P点的电势与Q点的电势相等 | D. | 带正电的微粒在O点的电势能为零 |
18.如图所示,质量分别为mA和mB的量物体A和B相对静止,以共同的速度沿斜面匀速下滑,则( )

| A. | A、B间无摩擦力的作用 | |
| B. | B受到斜面的滑动摩擦力的大小为(mA+mB)gsinθ | |
| C. | B受到物体A的静摩擦力的大小mAgsinθ | |
| D. | 取走物体A后,物体B仍能作匀速直线运动 |
 如图所示,甲、乙两列简谐横波均沿一匀质绳传播,其中甲沿+x方向传播(图中实线所示),乙沿-x方向传播(图中虚线所示),其波动频率相等且都为1Hz,振动方向均沿y轴,图示为t=0.5s时的波形.
如图所示,甲、乙两列简谐横波均沿一匀质绳传播,其中甲沿+x方向传播(图中实线所示),乙沿-x方向传播(图中虚线所示),其波动频率相等且都为1Hz,振动方向均沿y轴,图示为t=0.5s时的波形. 两个相同的薄壁型气缸A和B,活塞的质量都为m,横截面积都为S,气缸的质量都为M,$\frac{M}{m}$=$\frac{2}{3}$,气缸B的筒口处有卡环可以防止活塞离开气缸.将气缸B的活塞跟气缸A的气缸筒底用细线相连后,跨过定滑轮,气缸B放在倾角为30°的光滑斜面上,气缸A倒扣在水平地面上,气缸A和B内装有相同质量的同种气体,体积都为V0,温度都为27℃,如图所示,此时气缸A的气缸筒恰好对地面没有压力.设气缸内气体的质量远小于活塞的质量,大气对活塞的压力等于活塞重的1.5倍.求:
两个相同的薄壁型气缸A和B,活塞的质量都为m,横截面积都为S,气缸的质量都为M,$\frac{M}{m}$=$\frac{2}{3}$,气缸B的筒口处有卡环可以防止活塞离开气缸.将气缸B的活塞跟气缸A的气缸筒底用细线相连后,跨过定滑轮,气缸B放在倾角为30°的光滑斜面上,气缸A倒扣在水平地面上,气缸A和B内装有相同质量的同种气体,体积都为V0,温度都为27℃,如图所示,此时气缸A的气缸筒恰好对地面没有压力.设气缸内气体的质量远小于活塞的质量,大气对活塞的压力等于活塞重的1.5倍.求: 如图所示,水平圆盘可以绕中心轴转动,一质量为m的小物块放置在与中心转轴相距为r处,已知小物块与圆盘之间的动摩擦因数μ,假设最大静摩擦力等于滑动摩擦力,重力加速度为g,欲使小物块与圆盘保持相对静止,则圆盘匀速转动时的角速度不能超过$\sqrt{\frac{μg}{r}}$.
如图所示,水平圆盘可以绕中心轴转动,一质量为m的小物块放置在与中心转轴相距为r处,已知小物块与圆盘之间的动摩擦因数μ,假设最大静摩擦力等于滑动摩擦力,重力加速度为g,欲使小物块与圆盘保持相对静止,则圆盘匀速转动时的角速度不能超过$\sqrt{\frac{μg}{r}}$.