题目内容
19. 磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )
磁场具有能量,磁场中单位体枳内所具有的磁场能量叫磁场的能量密度,其表达式为ω=$\frac{{B}^{2}}{2μ}$,式中B磁感应强度,在空气中μ为一常量,一个学生根据能量守恒的思想来测量一条形磁铁N极端面附近的磁感应强度B的大小,他用一块与磁铁端面等大的铁片吸在磁铁上,然后用力缓慢拉开一段微小距离△x,如图所示,他测出磁铁端面的面面积为S,用力传感器测得拉力F的大小,己知拉力F做的功等于间隙中磁场的能量,则条形磁铁端面附近磁感应强B的大小可表示为( )| A. | $\sqrt{\frac{2μF}{S}}$ | B. | $\sqrt{\frac{2SF}{μ}}$ | C. | $\sqrt{\frac{μF}{S}}$ | D. | $\sqrt{\frac{SF}{μ}}$ |
分析 因为F所做的功等于△L间隙中磁场的能量,所以先分别求出F所做的功和△L间隙中磁场的能量,然后根据等量关系得出一等式,即可解得.
解答 解:在用力将铁片与磁铁拉开一段微小距离△L的过程中,拉力F可认为不变,因此F所做的功为:W=F•△L;
以ω表示间隙中磁场的能量密度,由题给条件ω=$\frac{{B}^{2}}{2μ}$,根据磁能量密度的定义可得:
△L间隙中磁场的能量为:E=ωV=$\frac{{B}^{2}}{2μ}$•S•△L;
由题意可知:F所做的功等于△L间隙中磁场的能量,即W=E;
则有:F•△L=$\frac{{B}^{2}}{2μ}$•S•△L
解得:B=$\sqrt{\frac{2μF}{S}}$.
故选:A.
点评 本题考查解磁能量密度,对于学生来说虽是一个新的物理量,但结合所学的密度不难解答;主要是正确理解磁能量密度的物理意义.

练习册系列答案
相关题目
4.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和环绕周期.由此可推算出( )
| A. | 行星的质量 | B. | 行星的线速度 | C. | 恒星的平均密度 | D. | 恒星的半径 |
7.如图,用绳子系一小球,使它在水平面内做匀速圆周运动,则( )


| A. | 重力对球做功,绳子的张力对球不做功 | |
| B. | 重力对球不做功,绳子的张力对球做功 | |
| C. | 重力和绳子的张力对球都不做功 | |
| D. | 重力和绳子对球都做功 |
14.氢原子第n能级的能量En=$\frac{{E}_{1}}{{n}^{2}}$,其中E1为基态能量,n=2,3,4,…现有一群氢原子从n=4的激发态自发地向较低能级跃迁,所发也的光子中波长最长的为λ0,则下列判断中正确的是( )
| A. | 这群氢原子跃迁过程中最多可放出3条不同频率的光谱线 | |
| B. | 波长为λ0的光子是氢原子从n=4的散发态直接跃迁到基态时发出的 | |
| C. | 用波长为λ0的光子照射处于基态的氢原子,不能使氢原子跃迁 | |
| D. | 用波长小于λ0的光子照射处于基态的氢原子,一定都能使氢原子电离 |
4.关于物理学史下列说法正确的是( )
| A. | 牛顿用放大法测出了引力常量 | |
| B. | 伽利略用理想实验证明了力是使物体运动的原因 | |
| C. | 楞次用归纳法得出了电磁感应的产生条件 | |
| D. | 库仑通过实验得出了库仑定律 |
9. 如图所示,光滑轻质挂钩下端悬挂质量为m的重物,跨在长度为L的轻绳上,开始时绳子固定在框架上等高的A、B两点,与水平方向的夹角为θ,绳子拉力为F.现保持绳长不变,将绳子右端从B点沿竖直方向缓慢移至C点,再从C点沿水平方向向左缓慢移至D点,关于绳子拉力F和重物重力势能Ep的变化,下列说法正确的是( )
如图所示,光滑轻质挂钩下端悬挂质量为m的重物,跨在长度为L的轻绳上,开始时绳子固定在框架上等高的A、B两点,与水平方向的夹角为θ,绳子拉力为F.现保持绳长不变,将绳子右端从B点沿竖直方向缓慢移至C点,再从C点沿水平方向向左缓慢移至D点,关于绳子拉力F和重物重力势能Ep的变化,下列说法正确的是( )
 如图所示,光滑轻质挂钩下端悬挂质量为m的重物,跨在长度为L的轻绳上,开始时绳子固定在框架上等高的A、B两点,与水平方向的夹角为θ,绳子拉力为F.现保持绳长不变,将绳子右端从B点沿竖直方向缓慢移至C点,再从C点沿水平方向向左缓慢移至D点,关于绳子拉力F和重物重力势能Ep的变化,下列说法正确的是( )
如图所示,光滑轻质挂钩下端悬挂质量为m的重物,跨在长度为L的轻绳上,开始时绳子固定在框架上等高的A、B两点,与水平方向的夹角为θ,绳子拉力为F.现保持绳长不变,将绳子右端从B点沿竖直方向缓慢移至C点,再从C点沿水平方向向左缓慢移至D点,关于绳子拉力F和重物重力势能Ep的变化,下列说法正确的是( )| A. | 从B移至C的过程中,拉力F保持不变 | |
| B. | 从B移至C的过程中,重力势能Ep逐渐变小 | |
| C. | 从C移至D的过程中,拉力F保持不变 | |
| D. | 从C移至D的过程中,重力势能Ep逐渐变小 |
 如图所示,有一轻质杆OA,可绕O点在竖直平面内自由转动,在杆的另一端A点和中点B各固定一质量为m的小球,设杆长为L,开始时杆静止在水平位置,求杆释放后,杆转到竖直位置时,A、B点两小球的重力势能减少了多少;A、B点两球的速度各是多大?
如图所示,有一轻质杆OA,可绕O点在竖直平面内自由转动,在杆的另一端A点和中点B各固定一质量为m的小球,设杆长为L,开始时杆静止在水平位置,求杆释放后,杆转到竖直位置时,A、B点两小球的重力势能减少了多少;A、B点两球的速度各是多大?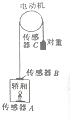 人们平常上下楼乘坐的电梯基本原理如图所示,钢缆缠绕在一个转轮上,牵引电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可以逆时针方向转动,这样在电动机带动下,轿厢可以上升,也可以下降.如果在电梯的轿厢地板上、牵引钢丝与轿厢连接处,牵引钢丝与对重连接处分别装有力传感器A、B、C.如图所示.某时刻电梯由低层从静止开始匀加速上升时,轿厢内只有一个乘客,乘客脚下的传感器A显示示数为660N,牵引钢丝与轿厢连接处的传感器B显示示数为13200N,牵引钢丝与对重连接处的传感器C显示示数为9000N.已知乘客质量为60kg,重力加速度g=10m/s2.求:
人们平常上下楼乘坐的电梯基本原理如图所示,钢缆缠绕在一个转轮上,牵引电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可以逆时针方向转动,这样在电动机带动下,轿厢可以上升,也可以下降.如果在电梯的轿厢地板上、牵引钢丝与轿厢连接处,牵引钢丝与对重连接处分别装有力传感器A、B、C.如图所示.某时刻电梯由低层从静止开始匀加速上升时,轿厢内只有一个乘客,乘客脚下的传感器A显示示数为660N,牵引钢丝与轿厢连接处的传感器B显示示数为13200N,牵引钢丝与对重连接处的传感器C显示示数为9000N.已知乘客质量为60kg,重力加速度g=10m/s2.求: 如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求:
如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求: