题目内容
3.甲和乙是绕某天体做匀速圆周运动的两颗卫星,甲的半径为r1,周期为T1,乙的周期为T2,且T1>T2,下列说法正确的是( )| A. | 甲的线速度较大 | |
| B. | 甲的向心加速度较大 | |
| C. | 利用所给条件可以求出天体的质量 | |
| D. | 利用所给条件可以求出天体的平均密度 |
分析 由开普勤第三定律分析卫星轨道半径的大小.据卫星的线速度公式v=$\sqrt{\frac{GM}{r}}$分析卫星线速度的大小,根据万有引力提供圆周运动的向心力,可求中心天体的质量.
解答 解:A、据题T1>T2,由开普勤第三定律知,r1>r2.据卫星的线速度公式v=$\sqrt{\frac{GM}{r}}$分析知,甲的线速度小,故A错误.
B、由G$\frac{Mm}{{r}^{2}}$=ma,得 a=$\frac{GM}{{r}^{2}}$,可知甲的向心加速度较小,故B错误.
C、由G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,可得天体的质量为 M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
已知卫星的轨道半径和周期,可求得天体的质量,故C正确.
D、由于天体的半径未知,所以不能求出天体的密度,故D错误.
故选:C.
点评 万有引力提供向心力是解决本题的关键,对于卫星的线速度公式要记住,选择题可直接运用.

练习册系列答案
相关题目
8. 如图所示,用平行于斜面的力F把质量为m的物体沿粗糙斜面上拉,斜面与水平面的夹角θ=30°,物体与斜面的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,并使其加速度大小等于该物体放在斜面上沿斜面下滑时的加速度大小,则F的大小是( )
如图所示,用平行于斜面的力F把质量为m的物体沿粗糙斜面上拉,斜面与水平面的夹角θ=30°,物体与斜面的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,并使其加速度大小等于该物体放在斜面上沿斜面下滑时的加速度大小,则F的大小是( )
 如图所示,用平行于斜面的力F把质量为m的物体沿粗糙斜面上拉,斜面与水平面的夹角θ=30°,物体与斜面的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,并使其加速度大小等于该物体放在斜面上沿斜面下滑时的加速度大小,则F的大小是( )
如图所示,用平行于斜面的力F把质量为m的物体沿粗糙斜面上拉,斜面与水平面的夹角θ=30°,物体与斜面的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,并使其加速度大小等于该物体放在斜面上沿斜面下滑时的加速度大小,则F的大小是( )| A. | $\frac{1}{4}$mg | B. | $\frac{1}{2}$mg | C. | mg | D. | $\frac{3}{4}$mg |
14.氢原子第n能级的能量En=$\frac{{E}_{1}}{{n}^{2}}$,其中E1为基态能量,n=2,3,4,…现有一群氢原子从n=4的激发态自发地向较低能级跃迁,所发也的光子中波长最长的为λ0,则下列判断中正确的是( )
| A. | 这群氢原子跃迁过程中最多可放出3条不同频率的光谱线 | |
| B. | 波长为λ0的光子是氢原子从n=4的散发态直接跃迁到基态时发出的 | |
| C. | 用波长为λ0的光子照射处于基态的氢原子,不能使氢原子跃迁 | |
| D. | 用波长小于λ0的光子照射处于基态的氢原子,一定都能使氢原子电离 |
12.“未觉池塘春草梦,阶前梧叶已秋声”.若一片梧桐叶从5m高的枝头自静止落至地面,所用时间可能为( )
| A. | 3s | B. | 1s | C. | 0.5s | D. | 0.2s |
13.下列关于超重与失重的说法,正确的是( )
| A. | 处于超重状态时,物体所受到的重力变大 | |
| B. | 处于失重状态时,物体所受到的重力变小 | |
| C. | 无论是超重或失重状态,物体所受到的重力并没有发生变化 | |
| D. | 处于完全失重状态时,物体所受到的重力为零 |
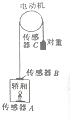 人们平常上下楼乘坐的电梯基本原理如图所示,钢缆缠绕在一个转轮上,牵引电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可以逆时针方向转动,这样在电动机带动下,轿厢可以上升,也可以下降.如果在电梯的轿厢地板上、牵引钢丝与轿厢连接处,牵引钢丝与对重连接处分别装有力传感器A、B、C.如图所示.某时刻电梯由低层从静止开始匀加速上升时,轿厢内只有一个乘客,乘客脚下的传感器A显示示数为660N,牵引钢丝与轿厢连接处的传感器B显示示数为13200N,牵引钢丝与对重连接处的传感器C显示示数为9000N.已知乘客质量为60kg,重力加速度g=10m/s2.求:
人们平常上下楼乘坐的电梯基本原理如图所示,钢缆缠绕在一个转轮上,牵引电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可以逆时针方向转动,这样在电动机带动下,轿厢可以上升,也可以下降.如果在电梯的轿厢地板上、牵引钢丝与轿厢连接处,牵引钢丝与对重连接处分别装有力传感器A、B、C.如图所示.某时刻电梯由低层从静止开始匀加速上升时,轿厢内只有一个乘客,乘客脚下的传感器A显示示数为660N,牵引钢丝与轿厢连接处的传感器B显示示数为13200N,牵引钢丝与对重连接处的传感器C显示示数为9000N.已知乘客质量为60kg,重力加速度g=10m/s2.求: 质量分别为3m和m的两个物体,用一根细绳相连,中间夹着一根被压缩的轻弹簧,在光滑水平地面上以速度υ0匀速运动,如图所示.某时刻剪断细线,质量为m的物体离开弹簧时的速度变为v=2υ0.求:
质量分别为3m和m的两个物体,用一根细绳相连,中间夹着一根被压缩的轻弹簧,在光滑水平地面上以速度υ0匀速运动,如图所示.某时刻剪断细线,质量为m的物体离开弹簧时的速度变为v=2υ0.求: 如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求:
如图所示,粗糙水平地面上固定着一个表面为光滑曲面的物体,该物体左下端与水平地面相切于A点,上部是半径为R的圆弧面,B为圆弧面的顶点,B点的高度为h.在水平地面上的O点放着一个质量为m的物块.O、A的距离为L.物块与地面间的动摩擦因数为μ,现对物体施加一个水平向右的恒力F,并在物体运动到OA段的中点时撤去F,物块经过A点后滑上光滑曲面,求: 如图所示,两平行光滑金属导轨竖直固定,边界水平的匀强磁场高度为h,方向垂直于导轨平面,两相同的导体棒a、b中点用长为h的绝缘轻杆相接,形成“工”字型框架,框架置于磁场上方,b棒距磁场上边界的高度为h,两棒与导轨接触良好.保持a、b棒水平,由静止释放框架,b棒刚进入磁场即做匀速运动,不计导轨电阻.则在框架下落过程中,b棒所受轻杆的作用力F及b棒的机械能E随下落的高度h变化的关系图象,可能正确的是( )
如图所示,两平行光滑金属导轨竖直固定,边界水平的匀强磁场高度为h,方向垂直于导轨平面,两相同的导体棒a、b中点用长为h的绝缘轻杆相接,形成“工”字型框架,框架置于磁场上方,b棒距磁场上边界的高度为h,两棒与导轨接触良好.保持a、b棒水平,由静止释放框架,b棒刚进入磁场即做匀速运动,不计导轨电阻.则在框架下落过程中,b棒所受轻杆的作用力F及b棒的机械能E随下落的高度h变化的关系图象,可能正确的是( )


