题目内容
15.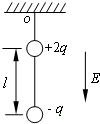 在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.
在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.
分析 根据库仑定律,及电场力公式,与矢量的合成法则,即可求解;
两个小球组成的整体为研究对象,分析受力,根据平衡条件可求得细线的拉力.
解答 解:根据库仑定律,则有:正电荷受到负电荷的库仑力,F1=$\frac{2k{q}^{2}}{{l}^{2}}$,
而正电荷受到匀强电场的电场力F2=2qE;
因两力方向相同,则正电荷所受电场力为F=$\frac{2k{q}^{2}}{{l}^{2}}$+2qE;
以整体为研究对象,受力分析可知受重力2mg,细绳的拉力T,有平衡条件得:
T=2mg
而库仑力为内力,
那么电场力F′=2qE-qE=qE;
得:T=2mg+qE.
因此细线对悬点 O 的作用力T′=2mg+qE
故答案为:$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,2mg+qE.
点评 本题要灵活运动隔离法和整体法对物体进行受力分析.运用整体法时,由于不分析两球之间的相互作用力,比较简便.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.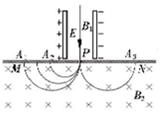 如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )
如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )
 如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )
如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )| A. | 磁感应强度为B1的磁场方向垂直纸面向外 | |
| B. | 能通过狭缝P的带电粒子的速度大小等于$\frac{E}{{B}_{1}}$ | |
| C. | 所有打在MN上的粒子,在磁感应强度为B2的磁场中的运动时间都相同 | |
| D. | 打在MN上的粒子位置离P越远,粒子的电荷量q越小 |
3.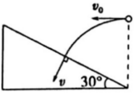 如图所示,斜面底端上方高h处有一小球以水平初速度v0抛出,恰好垂直打在斜面上,斜面的倾角为30°,则关于h和初速度v0的关系( )
如图所示,斜面底端上方高h处有一小球以水平初速度v0抛出,恰好垂直打在斜面上,斜面的倾角为30°,则关于h和初速度v0的关系( )
 如图所示,斜面底端上方高h处有一小球以水平初速度v0抛出,恰好垂直打在斜面上,斜面的倾角为30°,则关于h和初速度v0的关系( )
如图所示,斜面底端上方高h处有一小球以水平初速度v0抛出,恰好垂直打在斜面上,斜面的倾角为30°,则关于h和初速度v0的关系( )| A. | h=$\frac{{{v}_{0}}^{2}}{g}$ | B. | h=$\frac{{{3v}_{0}}^{2}}{2g}$ | C. | h=$\frac{{{2v}_{0}}^{2}}{g}$ | D. | h=$\frac{{{5v}_{0}}^{2}}{2g}$ |
10.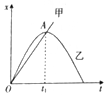 甲、乙两车同时由同一地点沿同一方向做直线运动,它们的位移-时间图象如图所示,甲车图象为过坐标原点的倾斜直线,乙车图象为顶点在A点的抛物线,则下列说法正确的是( )
甲、乙两车同时由同一地点沿同一方向做直线运动,它们的位移-时间图象如图所示,甲车图象为过坐标原点的倾斜直线,乙车图象为顶点在A点的抛物线,则下列说法正确的是( )
 甲、乙两车同时由同一地点沿同一方向做直线运动,它们的位移-时间图象如图所示,甲车图象为过坐标原点的倾斜直线,乙车图象为顶点在A点的抛物线,则下列说法正确的是( )
甲、乙两车同时由同一地点沿同一方向做直线运动,它们的位移-时间图象如图所示,甲车图象为过坐标原点的倾斜直线,乙车图象为顶点在A点的抛物线,则下列说法正确的是( )| A. | t1时刻甲车在乙车后方 | |
| B. | t=0时刻,乙的速度是甲的速度的两倍 | |
| C. | 0~t1时间段内甲、乙之间的距离一直增大 | |
| D. | 0~t1时间段乙的平均速度等于甲的平均速度 |
20.甲、乙两物体沿同直线同向同时运动,甲物体的位移与时间的关系满足x=16t-6t2(x的单位是m,t的单位是s),乙物体的速度与时间的关系满足v=4t2(v的单位是m/s,t的单位是s)则( )
| A. | 甲、乙两物体均做匀加速直线运动 | |
| B. | 甲、乙两物体均做匀减速直线运动 | |
| C. | 甲物体做匀减速直线运动,乙物体做非匀变速直线运动 | |
| D. | 甲物体的加速度大小为6m/s2 |
7.2016年9月25日,有着“超级天眼”之称的500米口径球面射电望远镜落成启用,为我国深空探索又推进了一大步.假如利用该“天眼”观察到两个未知天体A、B,其质量之比为MA:MB=2:3,半径之比为RA:RB=1:2,其周围各有一颗卫星,环绕天体A、B运行的卫星的轨道半径之比rA:rB=4:3,则下列选项正确的是( )
| A. | 两卫星受到的万有引力之比FA:FB=3:8 | |
| B. | 两卫星运动的向心加速度之比aA:aB=3:8 | |
| C. | 天体A、B的第一宇宙速度之比vA:vB=2$\sqrt{3}$:3 | |
| D. | 天体A、B表面的重力加速度之比gA:gB=3:8 |
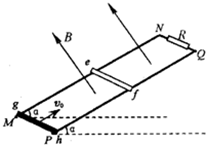 如图所示,两根平行金属导轨MN、PQ相距d=1.0m,导轨平面与水平面夹角α=30°,导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计.整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1.0T的匀强磁场中,金属棒ef垂直于MN、PQ静止放置,且与导轨保持良好接触,其长度刚好为d、质量m1=0.10kg、电阻r=0.40Ω,距导轨底端的距离s1=3.75m.另一根与金属棒平行放置的绝缘棒gh长度也为d,质量为m2=0.05kg,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑一段距离后再次静止,此过程中流过金属棒的电荷量q=0.1C且测得从碰撞至金属棒静止过程中金属棒上产生的焦耳热Q=0.05J.已知两棒与导轨间的动摩擦因数均为μ=$\frac{\sqrt{3}}{3}$,g=10m/s2.求:
如图所示,两根平行金属导轨MN、PQ相距d=1.0m,导轨平面与水平面夹角α=30°,导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计.整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1.0T的匀强磁场中,金属棒ef垂直于MN、PQ静止放置,且与导轨保持良好接触,其长度刚好为d、质量m1=0.10kg、电阻r=0.40Ω,距导轨底端的距离s1=3.75m.另一根与金属棒平行放置的绝缘棒gh长度也为d,质量为m2=0.05kg,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑一段距离后再次静止,此过程中流过金属棒的电荷量q=0.1C且测得从碰撞至金属棒静止过程中金属棒上产生的焦耳热Q=0.05J.已知两棒与导轨间的动摩擦因数均为μ=$\frac{\sqrt{3}}{3}$,g=10m/s2.求: 空间分布着沿水平方向垂直纸面向里、磁感应强度为B的匀强磁场,一个质量为m、电荷量为+q的小球套在竖直放置的、粗糙的长直杆上,t=0时刻给小球一个竖直向上的初速度v0,令其从O点向上运动,t=t1时刻小球运动到最高点A点(图中未画出),当小球返回O点时速率为v1,且在此之前小球已经做匀速运动,已知重力加速度为g,求:
空间分布着沿水平方向垂直纸面向里、磁感应强度为B的匀强磁场,一个质量为m、电荷量为+q的小球套在竖直放置的、粗糙的长直杆上,t=0时刻给小球一个竖直向上的初速度v0,令其从O点向上运动,t=t1时刻小球运动到最高点A点(图中未画出),当小球返回O点时速率为v1,且在此之前小球已经做匀速运动,已知重力加速度为g,求: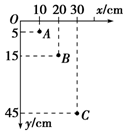 在“研究平抛物体的运动”的实验中
在“研究平抛物体的运动”的实验中