题目内容
20.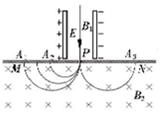 如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )
如图所示,若干个动量相同的带电粒子,先后沿直线通过由相互正交磁感应强度为B1的匀强磁场和电场强度为E的匀强电场组成的速度选择器,这些粒子通过平板MN上的狭缝P进入另一磁感应强度为B2的匀强磁场,最终落在平板MN上的A1~A3处,下列判断正确的是( )| A. | 磁感应强度为B1的磁场方向垂直纸面向外 | |
| B. | 能通过狭缝P的带电粒子的速度大小等于$\frac{E}{{B}_{1}}$ | |
| C. | 所有打在MN上的粒子,在磁感应强度为B2的磁场中的运动时间都相同 | |
| D. | 打在MN上的粒子位置离P越远,粒子的电荷量q越小 |
分析 带电粒子在速度选择器中做匀速直线运动,受力平衡,根据左手定则即可判断磁感应强度为B1的磁场方向;根据平衡方程即可求出粒子在速度选择器中的速度v;运用周期公式T=$\frac{2πR}{v}$,结合图中粒子在磁场中运动半径R的大小,即可用含R的式子表示出粒子在磁场中运动的时间;洛伦兹力提供向心力求出半径R,结合几何关系,运用控制变量法即可分析打在MN上的粒子位置离P的距离与电荷量q的关系.
解答 解:A、根据速度选择器中粒子所受电场力与洛伦兹力平衡,根据电场方向利用左手定则可知,磁感应强度为B1的磁场方向垂直纸面向外,故A正确;
B、根据速度选择器模型中,满足qvB1=Eq,所以可得带电粒子的速度大小v=$\frac{E}{{B}_{1}}$,故B正确;
C、所有打在MN上的粒子,都穿过速度选择器,所以粒子的速度均相同,且v=$\frac{E}{{B}_{1}}$,粒子在磁场中运动的周期T=$\frac{2πR}{v}$,由图可知打在A1、A2处粒子半径R不同,故粒子在磁场中运动的时间t=$\frac{T}{2}$=$\frac{πR}{v}$也不同,故C错误;
D、半径公式R=$\frac{mv}{q{B}_{2}}$,因为粒子动量P=mv均相同,打在MN上的粒子位置离P的距离d=2R=$\frac{2mv}{q{B}_{2}}$,所以可知d与q成反比,故打在MN上的粒子位置离P越远,粒子的电荷量q越小,故D正确;
故选:ABD
点评 本题为质谱仪模型,考查带电粒子在速度选择器中的运动和磁场中的运动,注意根据粒子运动形式选择合适的规律解决问题,要熟练掌握运用控制变量法结合半径公式R=$\frac{mv}{qB}$和周期公式T=$\frac{2πR}{v}$分析问题的方法.

 如图所示,M、N和P为“验证动量守恒定律”实验中小球的落点,已知入射球质量为m1,被碰球质量为m2,如果碰撞中动量守恒,则有( )
如图所示,M、N和P为“验证动量守恒定律”实验中小球的落点,已知入射球质量为m1,被碰球质量为m2,如果碰撞中动量守恒,则有( )| A. | m1•($\overrightarrow{OP}$-$\overrightarrow{OM}$)=m2•$\overrightarrow{ON}$ | B. | m1•($\overrightarrow{OP}$-$\overrightarrow{OM}$)=m2•$\overrightarrow{O′N}$ | C. | m1•($\overrightarrow{OP}$+$\overrightarrow{OM}$)=m2•$\overrightarrow{O′N}$ | D. | m1•$\overrightarrow{OP}$=m2•($\overrightarrow{O′N}$+$\overrightarrow{OM}$) |
 如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )
如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )| A. | A=0,B=0时Y=0 | B. | A=1,B=0时Y=1 | C. | A=0,B=1时Y=1 | D. | A=1,B=1时Y=1 |
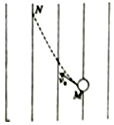 电子枪是加速电子轰击靶屏发光的一种装置,它发射出具有一定能量、一定束流以及速度和角度的电子束.电子束中某个电子只在电场力作用下从M点运动到N点的轨迹如图中虚线所示,图中一组平行实线可能是等势面也可能是电场线,则以下说法正确的是( )
电子枪是加速电子轰击靶屏发光的一种装置,它发射出具有一定能量、一定束流以及速度和角度的电子束.电子束中某个电子只在电场力作用下从M点运动到N点的轨迹如图中虚线所示,图中一组平行实线可能是等势面也可能是电场线,则以下说法正确的是( )| A. | 若图中实线是电场线,电子在M点的速度较大 | |
| B. | 若图中实线是电场线,M点的电势比N点低 | |
| C. | 不论图中实线是电场线还是等势面,电子在M点动能小 | |
| D. | 不论图中实线是电场线还是等势面,M点的场强都比N点小 |

| A. | 甲图用传感器观察震荡电流:回路电阻和向外辐射电磁波造成震荡电路能量的减小 | |
| B. | 乙图CT检查病人身体:CT是利用β射线照射人体 | |
| C. | 丙图检查平面表面平整度图样:利用光的干涉原理 | |
| D. | 丁图用激光打孔:利用激光具有高度相干性特点 |
| A. | 线速度 | B. | 向心加速度 | C. | 周期 | D. | 动能 |
| A. | 布朗运动是分子的运动 | |
| B. | 温度越高布朗运动越剧烈 | |
| C. | 温度高的物体一定比温度低的物体内能大 | |
| D. | 减小分子间的距离分子势能一定增大 |

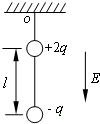 在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.
在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.