题目内容
7.2016年9月25日,有着“超级天眼”之称的500米口径球面射电望远镜落成启用,为我国深空探索又推进了一大步.假如利用该“天眼”观察到两个未知天体A、B,其质量之比为MA:MB=2:3,半径之比为RA:RB=1:2,其周围各有一颗卫星,环绕天体A、B运行的卫星的轨道半径之比rA:rB=4:3,则下列选项正确的是( )| A. | 两卫星受到的万有引力之比FA:FB=3:8 | |
| B. | 两卫星运动的向心加速度之比aA:aB=3:8 | |
| C. | 天体A、B的第一宇宙速度之比vA:vB=2$\sqrt{3}$:3 | |
| D. | 天体A、B表面的重力加速度之比gA:gB=3:8 |
分析 卫星绕行星做匀速圆周运动时,由万有引力提供向心力,由此列式得到向心加速度、第一宇宙速度的表达式,再求解向心加速度之比和第一宇宙速度之比.根据物体在行星表面时重力等于万有引力,列式分析天体A、B表面的重力加速度之比.
解答 解:A、设环绕天体A、B运行的卫星的质量分别为mA、mB.
由万有引力定律得:两卫星受到的万有引力之比 FA:FB=G$\frac{{M}_{A}{m}_{A}}{{R}_{A}^{2}}$:G$\frac{{M}_{B}{m}_{B}}{{R}_{B}^{2}}$,由于mA、mB关系未知,所以不能求出FA:FB.故A错误.
B、卫星绕行星做匀速圆周运动时,由万有引力提供向心力,得:
G$\frac{{M}_{A}{m}_{A}}{{r}_{A}^{2}}$=mAaA,G$\frac{{M}_{B}{m}_{B}}{{r}_{B}^{2}}$=mBaB.
可得 aA=G$\frac{{M}_{A}}{{r}_{A}^{2}}$,aB=G$\frac{{M}_{B}}{{r}_{B}^{2}}$
则aA:aB=G$\frac{{M}_{A}}{{r}_{A}^{2}}$:G$\frac{{M}_{B}}{{r}_{B}^{2}}$=3:8,故B正确.
C、根据万有引力等于向心力得:
G$\frac{{M}_{A}m}{{R}_{A}^{2}}$=m$\frac{{v}_{A}^{2}}{{R}_{A}}$,G$\frac{{M}_{B}m}{{R}_{B}^{2}}$=m$\frac{{v}_{B}^{2}}{{R}_{B}}$
可得 vA=$\sqrt{\frac{G{M}_{A}}{{R}_{A}}}$,vB=$\sqrt{\frac{G{M}_{B}}{{R}_{B}}}$
可得 vA:vB=2$\sqrt{3}$:3.故C正确.
D、物体在行星表面时重力等于万有引力,则有
G$\frac{{M}_{A}m}{{R}_{A}^{2}}$=mgA,G$\frac{{M}_{B}m}{{R}_{B}^{2}}$=mgB.
可得,天体A、B表面的重力加速度之比gA:gB=G$\frac{{M}_{A}}{{R}_{A}^{2}}$:G$\frac{{M}_{B}}{{R}_{B}^{2}}$=8:3,故D错误.
故选:BC
点评 对于卫星问题,关键是要熟练掌握万有引力提供卫星圆周运动的向心力,以及重力等于万有引力,并能写出向心力的不同表达式.

| A. | 线速度 | B. | 向心加速度 | C. | 周期 | D. | 动能 |
 图中虚线为匀强电场中与场强方向垂直的等间距平行直线,两粒子M、N质量相等,所带电荷的绝对值也相等,现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )
图中虚线为匀强电场中与场强方向垂直的等间距平行直线,两粒子M、N质量相等,所带电荷的绝对值也相等,现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )| A. | N从O点运动至a点时克服电场力做功 | |
| B. | N在a点的速率小于M在c点的速率 | |
| C. | M带正电荷,N带负电荷 | |
| D. | M从O点运动至b点时电场力对它做的功为零 |
| A. | 在摆长和时间的测量中,时间的测量对实验误差影响较大 | |
| B. | 在摆长和时间的测量中,长度的测量对实验误差影响较大 | |
| C. | 将振动次数n记为(n+1),测算出的g值比当地的公认值偏大 | |
| D. | 将摆线长当作摆长,未加摆球的半径测算出的g值比当地的公认值偏大 |
| A. | m1=m2,r1>r2 | B. | m1>m2,r1=r2 | ||
| C. | 降低斜槽的高度 | D. | 入射小球释放点要适当高一些 |
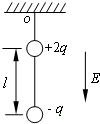 在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.
在场强为 E,方向竖直向下的匀强电场中,有两个质量均为 m 的带电 小球,电量分别为+2q 和-q,两小球用长为 l 的绝缘细线相连,另用绝缘 细线系住带正电的小球悬于 O 点,且处于平衡状态,重力加速度为g,则正电荷所受电场力为$\frac{2k{q}^{2}}{{l}^{2}}$+2qE,细线对悬点 O 的作用力等于2mg+qE.