题目内容
12. 如图所示,细绳一端系着一个质量为M=0.5kg的物体A,另一端通过光滑的小孔吊着质量为m=0.3kg的物体B,M的中点与圆孔的距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,若物体A相对水平面静止,物体B始终处于静止状态,平面转动的角速度ω最小值为$\sqrt{10}$rad/s,最大值为$5\sqrt{2}$rad/s (g=10m/s2)
如图所示,细绳一端系着一个质量为M=0.5kg的物体A,另一端通过光滑的小孔吊着质量为m=0.3kg的物体B,M的中点与圆孔的距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,若物体A相对水平面静止,物体B始终处于静止状态,平面转动的角速度ω最小值为$\sqrt{10}$rad/s,最大值为$5\sqrt{2}$rad/s (g=10m/s2)
分析 当角速度最小时,由于细绳的拉力作用,M有向圆心运动趋势,静摩擦力方向和指向圆心方向相反,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力.当角速度最大时,M有离开圆心趋势,静摩擦力方向指向圆心方向,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力.根据牛顿第二定律求解角速度的最大值和最小值.
解答 解:设物体M和水平面保持相对静止.
当ω具有最小值时,M有向圆心运动趋势,故水平面对M的静摩擦力方向和指向圆心方向相反,且等于最大静摩擦力2N.
根据牛顿第二定律隔离M有:
T-fm=Mω12r
解得ω1=$\sqrt{10}$rad/s
当ω具有最大值时,M有离开圆心趋势,水平面对M摩擦力方向指向圆心,大小也为2N.
再隔离M有:
T+fm=Mω22r
解得ω=$5\sqrt{2}$rad/s
故答案为:$\sqrt{10}$;$5\sqrt{2}$
点评 本题考查应用牛顿定律处理临界问题的能力.当物体将滑动时,静摩擦力达到最大值,解决连接体的物体时,找清连接体内的力的作用是解决此类物体的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
17.一个质量为m的小球固定在一根轻杆的一端,在竖直面内做圆周运动,当小球过最高点速度大小为v时,杆对小球的拉力为零.当小球过最高点速度大小为2v时,杆对小球的作用力大小和方向正确的是( )
| A. | 2mg,向上 | B. | 3mg,向上 | C. | 2mg,向下 | D. | 3mg,向下 |
4.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和环绕周期.由此可推算出( )
| A. | 行星的质量 | B. | 行星的线速度 | C. | 恒星的平均密度 | D. | 恒星的半径 |
1. 如图所示,质量分别为2m和m的两物块A、B,静止叠放在水平地面上,A、B间的动摩擦因数为2μ,B与地面间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力,A、B的接触面水平且B足够长,重力加速度为g.现对物块A施加一水平拉力F=7.5μmg,则物块B的加速度为( )
如图所示,质量分别为2m和m的两物块A、B,静止叠放在水平地面上,A、B间的动摩擦因数为2μ,B与地面间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力,A、B的接触面水平且B足够长,重力加速度为g.现对物块A施加一水平拉力F=7.5μmg,则物块B的加速度为( )
 如图所示,质量分别为2m和m的两物块A、B,静止叠放在水平地面上,A、B间的动摩擦因数为2μ,B与地面间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力,A、B的接触面水平且B足够长,重力加速度为g.现对物块A施加一水平拉力F=7.5μmg,则物块B的加速度为( )
如图所示,质量分别为2m和m的两物块A、B,静止叠放在水平地面上,A、B间的动摩擦因数为2μ,B与地面间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力,A、B的接触面水平且B足够长,重力加速度为g.现对物块A施加一水平拉力F=7.5μmg,则物块B的加速度为( )| A. | μg | B. | 1.5μg | C. | 2.5μg | D. | 3μg |
7.如图,用绳子系一小球,使它在水平面内做匀速圆周运动,则( )


| A. | 重力对球做功,绳子的张力对球不做功 | |
| B. | 重力对球不做功,绳子的张力对球做功 | |
| C. | 重力和绳子的张力对球都不做功 | |
| D. | 重力和绳子对球都做功 |
 2013年国际雪联越野滑雪中国巡回赛(简称TDSC)于1月2日在长春举行,如图所示,质量为60kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求:
2013年国际雪联越野滑雪中国巡回赛(简称TDSC)于1月2日在长春举行,如图所示,质量为60kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求: 滑板运动是一项非常刺激的水上运动.研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如图),滑板做匀速直线运动,相应的k=54kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin37°取$\frac{3}{5}$,忽略空气阻力):
滑板运动是一项非常刺激的水上运动.研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如图),滑板做匀速直线运动,相应的k=54kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin37°取$\frac{3}{5}$,忽略空气阻力): 为交流电流表.线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动.
为交流电流表.线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动.
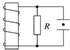 两块水平放置的金属板间距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量+q的油滴恰好处于静止,则线圈中的磁通量的变化率是$\frac{mgd(R+r)}{nqR}$.
两块水平放置的金属板间距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量+q的油滴恰好处于静止,则线圈中的磁通量的变化率是$\frac{mgd(R+r)}{nqR}$.