题目内容
5.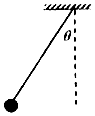 如图,长为L的细线悬挂一小球,小球的质量为m,使小球在竖直平面内运动,细线与竖直方向夹角为θ,则( )
如图,长为L的细线悬挂一小球,小球的质量为m,使小球在竖直平面内运动,细线与竖直方向夹角为θ,则( )| A. | θ最大时,细线对球的拉力小于mg | |
| B. | 只要θ≠0°,细线对球的拉力都小于mg | |
| C. | θ=0°时,细线对球的拉力等于mg | |
| D. | θ=0°时,细线对球的拉力小于mg |
分析 小球在竖直平面内做圆周运动,由指向圆心的合力充当向心力,分析受力情况,根据向心力知识分析.
解答 解:A、设细线对球的拉力为T.当θ最大时,球的速度为零,向心力为零,则有:T=mgcosθ,则T<mg,故A正确.
B、若θ≠0°,根据向心力知识有 T-mgcosθ=m$\frac{{v}^{2}}{L}$,得 T=mgcosθ+m$\frac{{v}^{2}}{L}$,可知,T不一定小于mg,T与球的速度有关,故B错误.
CD、当θ=0°时,根据向心力知识有 T-mg=m$\frac{{v}^{2}}{L}$,得 T=mg+m$\frac{{v}^{2}}{L}$,可知,T一定大于mg,故C、D错误.
故选:A
点评 在题是竖直平面内圆周运动问题,关键要明确向心力的来源:指向圆心的合力,由牛顿第二定律和向心力知识结合分析.

练习册系列答案
相关题目
15.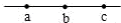 如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
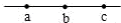 如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )| A. | b点的电势为-5V | |
| B. | a点的场强大于c点的场强 | |
| C. | 电场线的方向由a指向c | |
| D. | 正电荷由b点的电势能比在c点的电势能大 |
16.由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,则正确的结论是( )
| A. | 第1s末的速度为0.8m/s | B. | 加速度为0.8m/s2 | ||
| C. | 第2S内通过位移为1.2 m | D. | 2S内通过位移为1.2 m |
13.甲、乙两物体在t=0时的位置如图(a)所示,之后它们沿x轴正方向运动的速度图象如图(b)所示,则以下说法正确的有( )
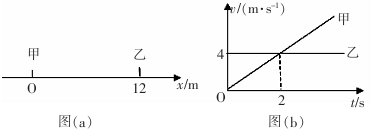

| A. | t=2s时甲追上乙 | |
| B. | 在前4s内甲乙两物体位移相等 | |
| C. | 甲追上乙之前两者间的最远距离为4m | |
| D. | 甲追上乙时的速度大小为8m/s |
20. 从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )
从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )
 从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )
从倾角为θ的足够长斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,不计空气阻力,下列关于小球的运动说法正确的是( )| A. | 小球两次落到斜面上时的速度方向相同 | |
| B. | 小球从抛出到落到斜面上所用时间相等 | |
| C. | 小球两次落到斜面上时的动能与抛出的初速度成正比 | |
| D. | 小球两次从抛出到落到斜面上的过程中所发生的位移与初速度的二次方成正比 |
10.探究力对原来静止的物体做的功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下: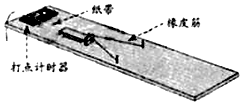
(1)设法让橡皮筋对小车做的功分别为W、2W、3W、…;
(2)分析打点计时器打出的纸带,求出小车的速度v1、v2、v3、…;
(3)作出W-v草图;
(4)分析W-v图象.如果W-v图象是一条直线,表明W∝v;如果不是直线,可考虑是否存在W∝v2、W∝v3、W∝$\sqrt{v}$等关系.
以下关于该实验的说法中有一项不正确,它是( )

(1)设法让橡皮筋对小车做的功分别为W、2W、3W、…;
(2)分析打点计时器打出的纸带,求出小车的速度v1、v2、v3、…;
(3)作出W-v草图;
(4)分析W-v图象.如果W-v图象是一条直线,表明W∝v;如果不是直线,可考虑是否存在W∝v2、W∝v3、W∝$\sqrt{v}$等关系.
以下关于该实验的说法中有一项不正确,它是( )
| A. | 本实验设法让橡皮筋对小车做的功分别为W、2W、3W、….所采用的方法是选用同样的橡皮筋,并在每次实验中使橡皮筋拉伸的长度保持一致.当用1条橡皮筋进行是实验时,橡皮筋对小车做的功为W,用2条、3条、…橡皮筋并在一起进行第2次、第3次、…实验时,橡皮筋对小车做的功分别是2W、3W、… | |
| B. | 小车运动中会受到阻力,补偿的方法,可以使木板适当倾斜 | |
| C. | 某同学在一次实验中,得到一条记录纸带.纸带上打出的点,两端密、中间疏.出现这种情况的原因,可能是没有使木板倾斜或倾角太小 | |
| D. | 根据记录纸带上打出的点,求小车获得的速度的方法,是以纸带上第一点到最后一点的距离来进行计算 |
17.从同样高度落下的玻璃杯,掉在水泥地上容易打碎,而掉在草地上不容易打碎,其原因是( )
| A. | 掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小 | |
| B. | 掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小 | |
| C. | 掉在水泥地上的玻璃杯动量改变慢,掉在草地上的玻璃杯动量改变快 | |
| D. | 掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢 |