题目内容
太阳系中某行星运行的轨道半径为R0,周期为T0.但科学家在长期观测中发现,其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星,则这颗未知行星运动轨道半径为
A.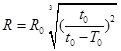 | B.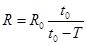 |
C.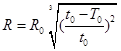 | D.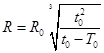 |
A
解析试题分析:据题意,已知每隔t0时间发生一次最大偏离,说明每隔t0时间两颗位于同一直线,据开普勒第三定律有: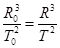 ,整理得:
,整理得: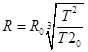 ,设某行星在t0时间内转动的角度为
,设某行星在t0时间内转动的角度为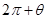 ,设其角速度为w0,则有:
,设其角速度为w0,则有: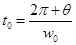 ,某行星在相同时间内转动的角度为
,某行星在相同时间内转动的角度为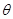 ,则有:
,则有: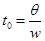 ,而
,而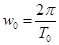 及
及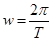 ,整理得
,整理得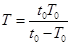 ,代入
,代入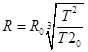 计算得:
计算得: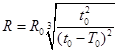 ,所以A选项正确。
,所以A选项正确。
考点:本题考查万有引力定律的应用。

练习册系列答案
相关题目
通常我们把太阳系中行星自转一周的时间称为“1天”,绕太阳公转一周的时间称为“1年”,已知金星的“1天”比它的“1年”还长。与地球相比较,金星的“1天”的时间约是地球 “1天”的时间的243倍。由此可知( )
| A.地球自转角速度约是金星自转角速度的243倍 |
| B.金星的质量约是地球质量的243倍 |
| C.金星的半径约是地球半径的243倍 |
| D.地球表面重力加速度约是金星表面的重力加速度的243倍 |
两颗人造地球卫星,质量之比m1:m2=1:2,轨道半径之比R1:R2=3:1,下面有关数据之比正确的是( )
| A.周期之比T1:T2=3:1 |
| B.线速度之比v1:v2=3:1 |
| C.向心力之比为F1:F2=1:9 |
| D.向心加速度之比a1:a2=1:9 |
发射地球同步卫星时,先将卫星发射至近地圆形轨道1,然后经点火使其沿椭圆轨道2运行,最后再次点火将卫星送入同步轨道3.轨道1、2相切于A点,轨道2、3相切于B点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
| A.卫星在轨道1上的运行速率大于轨道3上的速率 |
| B.卫星在轨道1上的角速度小于在轨道3上的角速度 |
| C.卫星在椭圆轨道2上经过A点时的速度大于7.9 km/s |
| D.卫星在椭圆轨道2上经过B点时的加速度等于它在轨道3上经过B点时的加速度 |
已知地球同步卫星到地球中心的距离为4.24×107m,地球自转的角速度为7.29×10-5rad/s,地面的重力加速度为9.8m/s2,月球到地球中心的距离为3.84×108m.假设地球上有一棵苹果树笔直长到了接近月球那么高,则当苹果脱离苹果树后,将( )
| A.沿着树干落向地面 |
| B.将远离地球,飞向宇宙 |
| C.成为地球的“苹果月亮” |
| D.成为地球的同步“苹果卫星” |
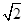 v1.已知某星球的半径为r,表面的重力加速度为地球表面重力加速度g的1/6,不计其它星球的影响,则该星球的第二宇宙速度为
v1.已知某星球的半径为r,表面的重力加速度为地球表面重力加速度g的1/6,不计其它星球的影响,则该星球的第二宇宙速度为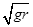
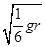
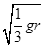
 gr
gr



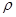 ,若由于星球自转使物体对星球表面的压力恰好为零,则星球自转的角速度为
,若由于星球自转使物体对星球表面的压力恰好为零,则星球自转的角速度为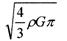
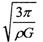
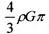
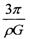
 。再经过两次轨道调整,最终进入100公里的近月圆轨道
。再经过两次轨道调整,最终进入100公里的近月圆轨道 ,轨道
,轨道