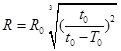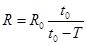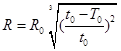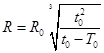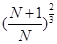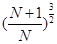题目内容
两颗人造地球卫星，质量之比m1：m2＝1:2，轨道半径之比R1:R2=3:1，下面有关数据之比正确的是( )
| A．周期之比T1:T2=3:1 |
| B．线速度之比v1:v2=3:1 |
| C．向心力之比为F1:F2=1:9 |
| D．向心加速度之比a1:a2=1:9 |
D
解析试题分析：据题意，已知人造地球卫星质量之比和轨道半径之比，则据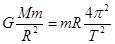
得
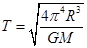，即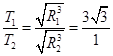
故A选项错误；据
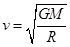可得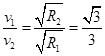
，故B选项错误；向心力与万有引力关系为：
，则有：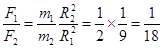
，故C选向南错误；由
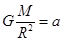可得：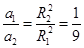
，故D选项正确。
考点：本题考查万有引力定律的应用。
每日10分钟口算心算速算天天练系列答案如图所示，a为地球赤道上的物体，b为沿地球表面附近做匀速圆周运动的人造卫星，c为地球同步卫星．关于a、b、c做匀速圆周运动的说法中正确的是（ ）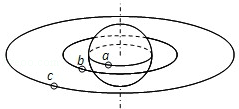
| A．角速度的大小关系为ωa=ωc＞ωb | B．向心加速度的大小关系为aa＞ab＞ac |
| C．线速度的大小关系为va＞vb＞vc | D．周期关系为Ta=Tc＞Tb |
2012年10月25日，我国第16颗北斗导航卫星升空，北斗卫星导航系统是继美GPS和俄GLONASS之后第三个成熟的卫星导航系统。这些卫星中含有地球轨道卫星、地球静止轨道卫星和倾斜地球同步轨道卫星，其中地球静止轨道卫星是位于赤道上空的同步卫星，倾斜地球同步轨道卫星的轨道平面与赤道平面有一定的夹角，其周期与地球自转周期相同。这些卫星的轨道均可看做圆。以下关于倾斜地球同步轨道卫星的说法正确的是
| A．如果它受到意外撞击速度变小，其轨道将变大 |
| B．它的运行速度比第一宇宙速度大 |
| C．它的向心加速度大小和位于赤道上空的同步卫星的向心加速度大小相等 |
| D．若倾斜角度适当，该卫星可以始终位于河南郑州的正上方 |
在发射地球同步卫星的过程中，卫星首先进入椭圆轨道Ⅰ，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道Ⅱ。若卫星的发射速度为v0，第一宇宙速度为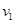
，在同步轨道Ⅱ上的运行速度为
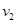，则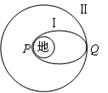
| A．v0＞＞ |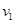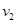
| B．若卫星的发射速度为2v0，卫星最终围绕地球运行的轨道半径将变大。 |
| C．在轨道Ⅰ上，卫星在P点的速度等于在Q点的速度 |
| D．卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ |
假设两颗“近地”卫星1和2的质量相同，都绕地球做匀速圆周运动，如图所示，卫星2的轨道半径更大些。两颗卫星相比较，下列说法中正确的是
| A．卫星1的向心加速度较小 |
| B．卫星1的动能较小 |
| C．卫星1的周期较小 |
| D．卫星1的机械能较小 |
如图所示是某卫星绕地飞行的三条轨道，轨道1是近地圆形轨道，2和3是变轨后的椭圆轨道。A点是2轨道的近地点，B点是2轨道的远地点，卫星在轨道1的的运行速率为7.7km/s，则下列说法中正确的是
| A．卫星在2轨道经过A点时的速率一定大于7.7km/s |
| B．卫星在2轨道经过B点时的速率可能大于7.7km/s |
| C．卫星在3轨道所具有的机械能等于2轨道所具有的机械能 |
| D．卫星分别在1、2轨道经过A点时的加速度相同 |
引力常量G=6.67×10-11N·m2/kg2，太阳光传到地球约需8分钟，试估算太阳与地球质量之和的数量级为
| A．1024kg | B．1027kg | C．1030kg | D．1035kg |