��Ŀ����
12��ͼ��EΪ��Դ���綯��E=330V�����費�ƣ�����R1=20k����R2=200k����ƽ�а�������峤l=18cm��������d=18cm��һ����������ӵ���q=8��10-15C������m=8��10-25kg����O1��������������O1O2��������䣬���ٶ�v0=3��106m/s������AB��CD���糡������CD�Ҳ���һ�̶�����������O2��ĵ���M�������ڽ���CD�Ҳ��˶������ж��ܱ��ֲ��䣮��֪������AB��CD���ΪS=27cm�������CD�Ҳ���ɵĵ糡�ֲ����ܽ����Ӱ�죬�������ӵ���������֪����������ΪK����
��1��ƽ�а�������������ĵ�ѹU
��2�����Ӵ�������CDʱƫ��������O1O2�ľ���L
��3�����ɵĵ���Q��
���� ��1���ɴ�������·�Ĺ��ɿ����ƽ�а���������˵ĵ�ѹֵ��
��2��������ƽ�а������������ƽ���˶������˶��ĺϳ���ֽ�������ֱ����ƫת��λ�ƺ��ٶȣ��ٶ�ƽ�а���Ĺ��̵�����ֱ���˶����з����������ƫ�����ĵľ��룻
��3��Ҫʹ���Ӷ��ܲ��䣬����ֻ��������Բ���˶����ɼ��ι�ϵ���ת���뾶�����ɿ������䵱�������������õ�����
��� �⣺��1��ƽ�а��������R2�����������ѹֵ����R2���˵ĵ�ѹ��
U=$\frac{E}{{R}_{1}+{R}_{2}}{R}_{2}$=$\frac{330}{20+200}��200$=300V��
��2�������ڵ糡������ƽ���˶������˶��ĺϳɺͷֽ��֪��
ˮƽ����l=v0t��
��ֱ�����ٶ�a=$\frac{Eq}{m}$=$\frac{Uq}{md}$
y=$\frac{1}{2}$$\frac{Uq}{md}$t2
������ã�y=$\frac{Uq{l}^{2}}{2md{v}_{0}^{2}}$=$\frac{300��8��1{0}^{-15}��0.1{8}^{2}}{2��8��1{0}^{-25}��9��1{0}^{12}}$��$\frac{1}{0.18}$=0.03m=3cm��
��ֱ����ķ��ٶ�Ϊ��vy=at=$\frac{Uql}{md{v}_{0}}$=$\frac{300��8��1{0}^{-15}��0.18}{8��1{0}^{-25}��0.18��3��1{0}^{6}}$=1��106m/s��
���Ӵ�AB����CD��ʱ��Ϊ��t1=$\frac{0.27}{3��1{0}^{6}}$=9��10-8s��
�����ӴﵽCDʱ��ֱ����ƫ����λ��Ϊ��y=0.03+vyt1=3+1��106��9��10-8=0.12m=12cm��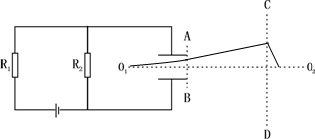 ��3��Ҫʹ���ӽ���CD�Ҳ���ܲ��䣬������һ����O2����Բ���˶����ɼ��ι�ϵ��֪����ת���뾶Ϊ��r=0.4m��
��3��Ҫʹ���ӽ���CD�Ҳ���ܲ��䣬������һ����O2����Բ���˶����ɼ��ι�ϵ��֪����ת���뾶Ϊ��r=0.4m��
ת�����ٶ�Ϊ��v=$\sqrt{��1��1{0}^{6}��^{2}+��3��1{0}^{6}��^{2}}$=$\sqrt{10}$��106m/s��
���ɿ�����������������֪��
$\frac{KQq}{{r}^{2}}=m\frac{{v}^{2}}{r}$
��ã�Q=$\frac{vr}{kq}$=$\frac{\sqrt{10}��1{0}^{6}��0.4}{9��1{0}^{9}��8��1{0}^{-15}}$=1.75��1010C��
�𣺣�1��ƽ�а�������������ĵ�ѹUΪ300V��
��2�����Ӵ�������CDʱƫ��������O1O2�ľ���LΪ12cm��
��3�����ɵĵ���QΪ1.75��1010C��
���� ���⿼����������ڴų��е��˶���Ҫע����ȷ������ƽ�а����ƽ���˶����뿪�����ֱ���˶����Կ��Էֽ�Ϊˮƽ����ֱ����������з������ƫתλ�ƣ�

 ��ͨ�����ֽ�����Ϊm�����壬�شֲڵ�б���ɾ�ֹ��ʼ�ȼ��ٵ��ɵ�����б�棬���������ĸ߶�Ϊh������б�涥�˵��ٶ�Ϊv����ͼ��ʾ�����ڴ˹����У�������
��ͨ�����ֽ�����Ϊm�����壬�شֲڵ�б���ɾ�ֹ��ʼ�ȼ��ٵ��ɵ�����б�棬���������ĸ߶�Ϊh������б�涥�˵��ٶ�Ϊv����ͼ��ʾ�����ڴ˹����У�������| A�� | �������ܵĺ���������Ϊmgh+$\frac{1}{2}$mv2 | |
| B�� | �������ܵĺ���������Ϊ$\frac{1}{2}$mv2 | |
| C�� | �˶��������Ĺ�Ϊmgh | |
| D�� | �˶��������Ĺ�����mgh |
 ��ͼ��ʾ���ڰ뾶ΪR��Բ�������ڣ�Բ��ΪO������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱ��Բƽ�棨δ��������һȺ������ͬ�Ⱥɵĸ���������ͬ��������P����ֽƽ������ͬ��������ų��У�����ƫת���ַɳ��ų����������ڴų����˶��Ĺ���뾶����R��������˵������ȷ���ǣ��������ӵ���������������
��ͼ��ʾ���ڰ뾶ΪR��Բ�������ڣ�Բ��ΪO������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱ��Բƽ�棨δ��������һȺ������ͬ�Ⱥɵĸ���������ͬ��������P����ֽƽ������ͬ��������ų��У�����ƫת���ַɳ��ų����������ڴų����˶��Ĺ���뾶����R��������˵������ȷ���ǣ��������ӵ���������������| A�� | ��Q��ɳ��������ڴų����˶���ʱ��� | |
| B�� | ��PQ������������ӷɳ�ʱƫת����� | |
| C�� | �������ӷɳ��ų�ʱ�Ķ���һ����� | |
| D�� | �ڴų����˶�ʱ��������Ӳ����ܾ���Բ��O�� |
 ��ͼ��ʾ����ֱ��������AOCΪ�߽�Ĵ�ֱֽ��������н���ǿ�ų����Ÿ�Ӧǿ��ΪB����A=60�㣬AO=a����O�����һ������Դ�����������������ij�ִ��������ӣ����ӵıȺ�Ϊ$\frac{q}{m}$�������ٶȴ�С��Ϊv0��������v0=$\frac{qBa}{m}$�����䷽����ͼ�еĽǶȦȱ�ʾ��0��ܦȡ�90�㣩���������ӽ���ų�����˶��������������ã�������˵����ȷ���ǣ�������
��ͼ��ʾ����ֱ��������AOCΪ�߽�Ĵ�ֱֽ��������н���ǿ�ų����Ÿ�Ӧǿ��ΪB����A=60�㣬AO=a����O�����һ������Դ�����������������ij�ִ��������ӣ����ӵıȺ�Ϊ$\frac{q}{m}$�������ٶȴ�С��Ϊv0��������v0=$\frac{qBa}{m}$�����䷽����ͼ�еĽǶȦȱ�ʾ��0��ܦȡ�90�㣩���������ӽ���ų�����˶��������������ã�������˵����ȷ���ǣ�������| A�� | �����ڴų����˶��ʱ��Ϊ$\frac{��m}{3qB}$ | |
| B�� | �Ԧ�=60�����������ڴų����˶���ʱ����� | |
| C�� | �Ԧȣ�30�����������ڴų����˶���ʱ�䶼��� | |
| D�� | ��AC�߽���ֻ��һ��������������� |
 ��ͼ��ʾ����xOyƽ���ڵ�y�������֮�����Բ��������Ŀռ������ǿ�ų����ų�����ֱֽ�����⣬�Ÿ�Ӧǿ�ȴ�СΪB�����߾���Q�㣨3L��0������y��ƽ�У�Բ�������Բ��P������Ϊ��2L��0�����뾶ΪL��һ������Ϊm�������Ϊq�Ĵ���������Ӵ�y����ij�㴹ֱy�����ų����������ӵ�������������
��ͼ��ʾ����xOyƽ���ڵ�y�������֮�����Բ��������Ŀռ������ǿ�ų����ų�����ֱֽ�����⣬�Ÿ�Ӧǿ�ȴ�СΪB�����߾���Q�㣨3L��0������y��ƽ�У�Բ�������Բ��P������Ϊ��2L��0�����뾶ΪL��һ������Ϊm�������Ϊq�Ĵ���������Ӵ�y����ij�㴹ֱy�����ų����������ӵ�������������| A�� | �������û�о���Բ��������Q�㣬�����ӵ������ٶ�Ϊv=$\frac{3qBL}{m}$ | |
| B�� | �������û�о���Բ��������Q�㣬�����ӵ������ٶ�Ϊv=$\frac{3qBL}{2m}$ | |
| C�� | ���ӵ�һ�δ�P�㾭����x�ᣬ�����ӵ���С�����ٶ�Ϊvmin=$\frac{\sqrt{3}qBL}{m}$ | |
| D�� | ���ӵ�һ�δ�P�㾭����x�ᣬ�����ӵ���С�����ٶ�Ϊvmin=$\frac{2qBL}{m}$ |
 ��ͼ��ʾ����бֱ���AB���30�㣬����s1=1.8m����Ħ��������1=$\frac{\sqrt{3}}{6}$��ˮƽ���BC��DE��FG���⻬��DE��Ϊs2=1m����б�����ˮƽ�����B���Թ⻬СԲ��ƽ�����ӣ�С������m2=4kg����ΪL=0.8m���ϱ��涯Ħ��������2=0.4���ϱ�����BC��FG����ȸߣ���С������EF��������ʱ����ֹͣ�˶�����ʼС���������CD���浫��CD���治���ӣ�С����m1����Ϊ�ʵ㣬����б�������A��ֹ�ͷţ�g=10m/s2����
��ͼ��ʾ����бֱ���AB���30�㣬����s1=1.8m����Ħ��������1=$\frac{\sqrt{3}}{6}$��ˮƽ���BC��DE��FG���⻬��DE��Ϊs2=1m����б�����ˮƽ�����B���Թ⻬СԲ��ƽ�����ӣ�С������m2=4kg����ΪL=0.8m���ϱ��涯Ħ��������2=0.4���ϱ�����BC��FG����ȸߣ���С������EF��������ʱ����ֹͣ�˶�����ʼС���������CD���浫��CD���治���ӣ�С����m1����Ϊ�ʵ㣬����б�������A��ֹ�ͷţ�g=10m/s2���� ��ͼ���������̵ĵ���������ʹ��a��b�����˵�ʱ����Ϊ1A����ʹ��a��c�����˵�ʱ����Ϊ0.1A����֪��ͷ������RgΪ200������ƫ����IgΪ2mA����R1=0.41����R2=3.67���������վ�������λС����
��ͼ���������̵ĵ���������ʹ��a��b�����˵�ʱ����Ϊ1A����ʹ��a��c�����˵�ʱ����Ϊ0.1A����֪��ͷ������RgΪ200������ƫ����IgΪ2mA����R1=0.41����R2=3.67���������վ�������λС���� �뾶Ϊr������ΪI1��ͨ��Բ��Բ��a���ĴŸ�Ӧǿ��ΪB����Բ���·���Բ��aΪL�ĵط�ˮƽ����һ������ΪI2������ֱ����MNʱ��Բ��Բ��a���ĴŸ�Ӧǿ�ȱ�Ϊ�㣬��Բ��ƽ���볤ֱ������ͬһ��ֱƽ������ͼ��ʾ����
�뾶Ϊr������ΪI1��ͨ��Բ��Բ��a���ĴŸ�Ӧǿ��ΪB����Բ���·���Բ��aΪL�ĵط�ˮƽ����һ������ΪI2������ֱ����MNʱ��Բ��Բ��a���ĴŸ�Ӧǿ�ȱ�Ϊ�㣬��Բ��ƽ���볤ֱ������ͬһ��ֱƽ������ͼ��ʾ����