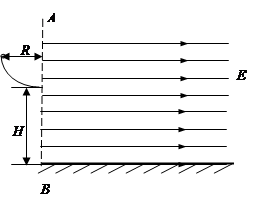题目内容
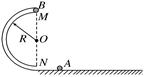
(16分)如图所示,ABC为光滑轨道,其中AB段水平,BC段是半径为R的圆弧,AB与BC相切于B点,A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧处于原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处,但不挤压.现使一质量为m的小球从圆弧轨道上距水平轨道高h处的D点由静止下滑,小球与物块相碰后立即有相同速度但不粘连,此后物块与L形挡板相碰后速度立即减为0也不粘连.(整个过程,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g.)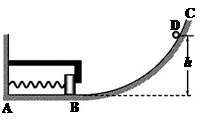
(1)试求弹簧获得的最大弹性势能;
(2)求小球与物块第一次碰后沿BC上升的最大高度;
⑴ 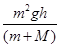 ⑵
⑵ 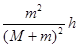
解析试题分析:小球先从曲面滑下,该过程满足机械能守恒,然后与物块碰撞满足动量守恒,接着和物块一起压缩弹簧至最短然后弹回到物块与L形挡板相碰,这个过程小球、物块和弹簧系统机械能守恒,最后小球与物块分离滑上曲面,该过程小球机械能守恒。
⑴球从D下滑到B与物块碰前,小球机械能守恒: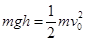 (3分)
(3分)
碰撞过程,小球与滑块系统动量守恒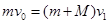 (3分)
(3分)
碰后弹簧压缩到最大程度的过程中,M、m和弹簧的系统机械能守恒 (2分)
(2分)
解得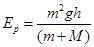 (2分)
(2分)
⑵第一次碰后,小球返回B点的速度仍为v1,设从B向C滑动的最大高度为h1,有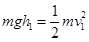 (3分)
(3分)
则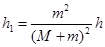 (3分)
(3分)
考点:本题考查机械能守恒、动量守恒定律的应用以及多个运动过程的分析计算等。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A.曲线运动一定是变速运动 |
| B.物体只有受到一个方向不断改变的力,才可能做曲线运动 |
| C.匀速圆周运动的加速度保持不变 |
| D.两个直线运动的合运动一定是直线运动 |

 ;
; ;
;
 (q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求:
(q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求: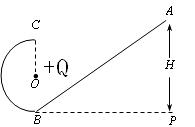


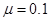 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?