Question

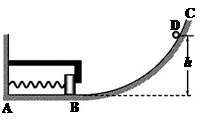
如图所示，在虚线AB的左侧固定着一个半径R=0.2m的1/4光滑绝缘竖直轨道，轨道末端水平，下端距地面高H=5m，虚线AB右侧存在水平向右的匀强电场，场强E=2×10³ V/m。有一带负电的小球从轨道最高点由静止滑下，最终落在水平地面上，已知小球的质量m=2g，带电量q=1×10^-6 C,小球在运动中电量保持不变，不计空气阻力（取g=10m/s²）求：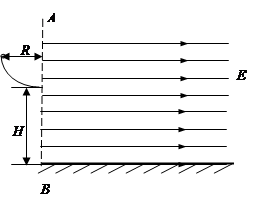

（1）小球落地的位置离虚线AB的距离；
（2）小球落地时的速度。

Answer 1

1.5m 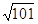 m/s    tanθ=10     θ=arctan10(与水平方向夹角)

解析试题分析：小球进入磁场以后的运动可分解为水平方向的匀变速直线运动和竖直方向上的自由落体运动，可根据机械能守恒定律求出水平方向的初速度，然后根据自由落体运动求出时间，从而求出水平位移，以及两个方向上的末速度，再求出合速度大小。
（1）根据机械能守恒得mgR= 则 v₀=2m/s     
而小球在空中运动的时间 t==1s
水平方向上的加速度a_x=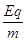=1m/s²   
故水平位移S_x=v₀t-=1.5m
落地时水平速度 v_x=v₀-at=1m/s   
竖直速度v_y="gt=10m/s" 则合速度v_t==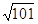m/s  
tanθ=10，θ=arctan10(与水平方向夹角)
考点：机械能守恒，速度的合成与分解