题目内容
(18分)如图所示,质量为M的厚壁塑料管B内有一个质量为m的小塑料球A,塑料球A的直径略小于塑料管B的内径,且M ≥m; A和B之间有一根极短的轻弹簧,轻弹簧与A、B不连接。将此装置从B下端离地板的高度H处由静止释放,B触地后在极短时间内反弹,且其速度大小不变,接着A脱离B竖直上升,而B恰好停留在地板上。不计空气阻力及A与B内壁的摩擦。求:
(1)塑料球A上升的高度;
(2)弹簧中能达到的最大弹性势能。
①若M=m,A上升的高度 ;弹簧能达到的最大弹性势能
;弹簧能达到的最大弹性势能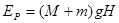 。
。
②若M>m,A上升的高度为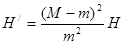 ;弹簧能达到的最大弹性势能
;弹簧能达到的最大弹性势能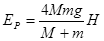 。
。
解析试题分析:(1)A和B一起自由下落H,处于完全失重状态,轻弹簧处于原长,A和B一起下落,满足机械能守恒: 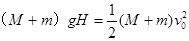 2分
2分
解得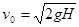 1分
1分
B自地面原速反弹后,A和B组成的系统动量守恒,以向上为矢量正方向,有:
①若M=m,有: 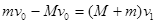 2分
2分
解得v1=0 1分
在此条件下,A和B的初动能完全转化成弹簧的弹性势能,有: 1分
1分
弹簧弹开A和B,B静止在地面,A竖直上升,弹性势能转化为A的重力势能,有: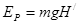 1分
1分
解得A上升的高度 1分
1分
②若M>m,有: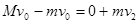 2分
2分
解得A上升的初速度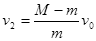 1分
1分
可得A上升的高度为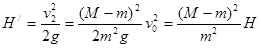 1分
1分
在A离开弹簧之前的某一时刻,A和B的速度大小相等时,弹簧的弹性势能最大,有: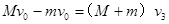 1分
1分
从A开始压缩弹簧到A和B速度相等,满足机械能守恒,有: 1分
1分
解得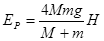 1分
1分
综上所述:①若M=m,A上升的高度 ;弹簧能达到的最大弹性势能
;弹簧能达到的最大弹性势能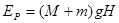 。
。
②若M>m,A上升的高度为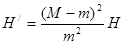 ;弹簧能达到的最大弹性势能
;弹簧能达到的最大弹性势能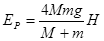 。
。
综上所述部分正确再给 2分
考点:机械能守恒

 阅读快车系列答案
阅读快车系列答案炮弹从炮口射出时的速度大小为v,方向与水平方向成 角,如图所示,把这个速度沿水平和竖直方向分解,则竖直分速度的大小是( )
角,如图所示,把这个速度沿水平和竖直方向分解,则竖直分速度的大小是( )
| A.vsinα | B.vcosα | C.v/sinα | D.v/cosα |

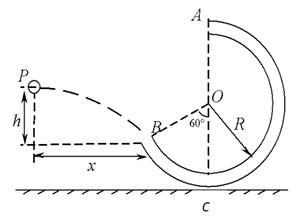
 x0.求M与m的关系式。
x0.求M与m的关系式。