题目内容
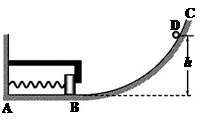
(12分)如图所示,在竖直平面内的轨道,AB段粗糙且绝缘,BC段为半径为R的光滑绝缘圆弧轨道,半径OC竖直。圆心O点处有一带电量为Q的正点电荷。一个质量为m带电量为 (q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求:
(q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求: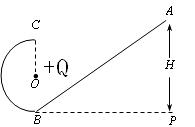
(1)小球到达C点时速度大小;
(2)小球到达B点时动能大小;
(3)摩擦力对小球做的功(提示:取无穷远处电势为零,离点电荷Q距离为r处的电势为φ="kQ/r" )。
(1)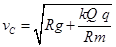 ;(2)
;(2) ;(3)
;(3)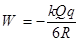
解析试题分析:(1)小球到达最高点时对轨道没有压力,则: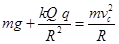 (2分)
(2分)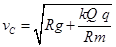 (2分)
(2分)
(2)小球在圆轨道运动过程中,只有重力做功,机械能守恒,设B点处为零势能面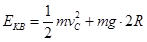 (2分)
(2分) (2分)
(2分)
(3)小球在AB段运动过程,由能量守恒可知摩擦力做的功为: (2分)
(2分)
代入得: 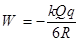 (2分)
(2分)
考点:圆周运动、机械能守恒定律、能量守恒

练习册系列答案
相关题目