题目内容

（9分）如图所示，圆管构成的半圆形轨道竖直固定在水平地面上，轨道半径为R，MN为直径且与水平面垂直，直径略小于圆管内径的小球A以某一速度冲进轨道，到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞，碰后两球粘在一起飞出轨道，落地点距N为2R。重力加速度为g，忽略圆管内径，空气阻力及各处摩擦均不计。求：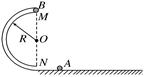

①粘合后的两球从飞出轨道到落地的时间t；
②小球A冲进轨道时速度v的大小。

①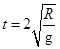　②

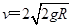
解析试题分析：①粘合后的两球从飞出轨道到落地做平抛运动，由平抛运动知识得，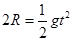
，所以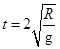
②设球A的质量为m，碰撞前速度大小为v1，把球A冲进轨道最低点时的重力势能定为0，由机械能守恒定律知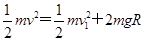③
设碰撞后粘合在一起的两球速度大小为v2，由动量守恒定律知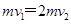④
飞出轨道后做平抛运动，水平方向分运动为匀速直线运动，有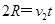⑤
综合②③④⑤式得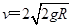 ⑥
考点：考查了平抛运动，机械能守恒，动量守恒定律的综合应用

练习册系列答案
相关题目

下列情况中，运动物体机械能一定守恒的是

A．作匀速直线运动的物体 B．作平抛运动的物体
C．物体不受摩擦力的作用 D．物体只受重力的作用

如图所示，光滑水平面上放有A、B、C三个物块，其质量分别为mA=2.0kg，mB=mC=1.0kg，用一轻弹簧固接A、B两物块，B、C只是靠在一起．现用力压缩弹簧使三物块靠近，此过程外力做功72J，然后释放，求：

（1）释放后物块B对物块C一共做了多少功？
（2）弹簧第二次被压缩时，弹簧具有的最大弹性势能为多大？

如图所示，一不可伸长的轻绳上端悬挂于O点，下端系一质量m=1.0kg的小球。现将小球拉到A点（保持绳绷直）由静止释放，当它经过B点时绳恰好被拉断，小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上，已知绳长L=1.0m，B点离地高度H=1.0m，A、B两点的高度差h=0.5m，重力加速度g取10m/s2，不计空气阻力影响，求：

（1）地面上DC两点间的距离s；
（2）轻绳所受的最大拉力大小。

（16分）质量为m的钢板与直立轻弹簧的上端连接，弹簧下端固定在地上．平衡时， 弹簧的压缩量为x0，如右图所示．一物块从钢板正上方距离为3x0的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连．它们到达最低点后又向上运动．已知物块质量也为m时，它们恰能回到O点．若物块质量为M，仍从A处自由落下，则物块与钢板回到O点时，还具有向上的速度．物块向上运动到达的最高点与O点的距离h＝x0．求M与m的关系式。

（8分）如图所示，有一光滑的半径可变的1/4圆形轨道处于竖直平面内，圆心O点离地高度为H.现调节轨道半径，让一可视为质点的小球a从与O点等高的轨道最高点由静止沿轨道下落，使小球离开轨道后运动的水平位移S最大，求小球脱离轨道最低点时的速度大小。

（10分）如图所示，一质量为M的滑块静止在光滑的水平面上，其左侧是一光滑的四分之一圆弧，圆弧半径为R=1m，一质量为m的小球以速度V0向右运动冲上滑块，已知M=4m，g取10 m/s2，若小球刚好没跃出圆弧的上端，求：

①小球的初速度V0是多少?  
②滑块获得的最大速度是多少?

（16分）如图所示，ABC为光滑轨道，其中AB段水平，BC段是半径为R的圆弧，AB与BC相切于B点，A处有一竖直墙面，一轻弹簧的一端固定于墙上，另一端与一质量为M的物块相连接，当弹簧处于原长状态时，物块恰能与固定在墙上的L形挡板相接触于B处，但不挤压．现使一质量为m的小球从圆弧轨道上距水平轨道高h处的D点由静止下滑，小球与物块相碰后立即有相同速度但不粘连，此后物块与L形挡板相碰后速度立即减为0也不粘连．（整个过程，弹簧没有超过弹性限度，不计空气阻力，重力加速度为g.）

（1）试求弹簧获得的最大弹性势能；
（2）求小球与物块第一次碰后沿BC上升的最大高度；

（1）（6分）氢原子的能级如图所示。氢原子从n=3能级向n=l能级跃迁所放出的光子，恰能使某种金属产生光电效应，则该金属的截止频率为____Hz；用一群处n=4能级的氢原子向低能级跃迁时所发出的光照射该金属，产生的光电子最大初动能为____ eV（普朗克常量h=6．63×10-34J'·s，结果均保留2位有效数字）。

（2）（9分）如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内．a、b是轨道的两端点且高度相同，O为圆心。小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰。第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）。求A、B两球的质量之比mA:mB。（结果可以用根式表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网