题目内容
16.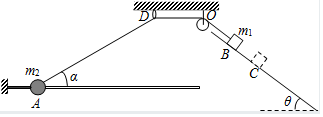 如图所示,一根不可伸长的轻细绳穿过光滑小环D,绕过轻质光滑定滑轮O,一端与物块m1连接,另一端与穿在光滑水平细杆上的小球m2连接,m2左端通过水平细线固定在竖直墙壁上,整个装置在同一竖直平面内.当m2静止在A点时,轻细绳与水平面的夹角为α=30°,D、A间的距离为1.2m.已知斜面倾角θ=37°,m1=2kg,m2=1kg,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,细杆、斜面足够长.求:
如图所示,一根不可伸长的轻细绳穿过光滑小环D,绕过轻质光滑定滑轮O,一端与物块m1连接,另一端与穿在光滑水平细杆上的小球m2连接,m2左端通过水平细线固定在竖直墙壁上,整个装置在同一竖直平面内.当m2静止在A点时,轻细绳与水平面的夹角为α=30°,D、A间的距离为1.2m.已知斜面倾角θ=37°,m1=2kg,m2=1kg,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,细杆、斜面足够长.求:(1)水平细线对小球的拉力大小;
(2)若将水平细线剪断,小球运动的最大速度;
(3)将水平细线剪断后,物块m1从B点沿斜面运动0.4m到C时的速度.
分析 (1)分别对两物体受力分析,由平衡条件列方程求解;
(2)小球速度最大时,正好在D点正下方,由机械能守恒定律列方程求解;
(3)由速度的合成与分解得到两个物块速度的关系,对系统由机械能守恒定律列方程求解.
解答 解:(1)分析A、B受力如图,由平衡条件可知:
对m2有:T2=T1cosα
对m1有:T1=m1gsinθ
联立以上各式并代入数据得:T2=6$\sqrt{3}$N
(2)小球速度最大时,正好在D点正下方,m1速度为零,
对系统由机械能守恒得:$\frac{1}{2}$m2${v}_{m}^{2}$=m1g($\overline{AD}$-$\overline{AD}$ sinα)sinθ
代入数据得:vm=$\frac{6\sqrt{10}}{5}$m/s
(3)设物块运动到C时,小球运动到E,此时绳与细杆间的夹角为β,
由数学知识可知sinβ=$\frac{\overline{AD}sinα}{\overline{AD}-\overline{BC}}$,sin2β+cos2β=1,cosβ=$\frac{\sqrt{7}}{4}$
m1从B滑到C的速度为v1.由系统由机械能守恒得:$\frac{1}{2}$m1 ${v}_{1}^{2}$+$\frac{1}{2}$m2${v}_{2}^{2}$=m1g$\overline{BC}$ sinθ
由速度分解知识可得:v1=v2cosβ
联立以上各式并代入数据得:v1=$\frac{2\sqrt{14}}{5}$ m/s
答:(1)水平细线对小球的拉力大小为6$\sqrt{3}$N;
(2)若将水平细线剪断,小球运动的最大速度$\frac{6\sqrt{10}}{5}$m/s;
(3)将水平细线剪断后,物块m1从B点沿斜面运动0.4m到C时的速度$\frac{2\sqrt{14}}{5}$ m/s.
点评 解决“绳(杆)端速度分解模型”问题时应把握以下两点:
(1)确定合速度,它应是m2的实际速度;
(2)m2运动引起了两个效果:一是左边绳子的缩短,二是绳绕滑轮的转动.应根据实际效果进行运动的分解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 奥斯特在实验中观察到电流的磁效应,该效应说明了电和磁之间存在联系 | |
| B. | 法拉第根据通电直导线的磁场和条形磁铁的磁场的相似性,提出了分子电流假说 | |
| C. | 安培在实验中观察到,通有恒定电流的静止导线附近的固定导线圈中,出现了感应电流 | |
| D. | 楞次在分析了许多实验事实后提出,感应电流应具有这样的方向,即感应电流的磁场总是与引起感应电流的磁场方向相反 |
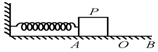 如图所示,轻弹簧一端固定,另一端自由伸长时恰好到达O点,将质量为m(视为质点)的物体P与弹簧连接,并将弹簧压缩到A由静止释放物体后,物体将沿水平面运动到B点.若物体与水平面的摩擦力不能忽略,则关于物体运动的下列说法中正确的是( )
如图所示,轻弹簧一端固定,另一端自由伸长时恰好到达O点,将质量为m(视为质点)的物体P与弹簧连接,并将弹簧压缩到A由静止释放物体后,物体将沿水平面运动到B点.若物体与水平面的摩擦力不能忽略,则关于物体运动的下列说法中正确的是( )| A. | A到O速度不断增大,O到B速度不断减小 | |
| B. | A到O速度先增大后减小,O到B速度不断减小 | |
| C. | A到O加速度减小,O到B加速度不断增大 | |
| D. | A到O加速度增大,O到B加速度不断减小 |
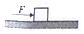 如图所示,水平地面上质量m=1kg的物体,在F=2N的水平推力的作用力下以a=1m/s2的加速度做匀加速运动.取g=10m/s2,若不改变推力的方向,把推力的大小增大到4N,则物体的加速度大小为( )
如图所示,水平地面上质量m=1kg的物体,在F=2N的水平推力的作用力下以a=1m/s2的加速度做匀加速运动.取g=10m/s2,若不改变推力的方向,把推力的大小增大到4N,则物体的加速度大小为( )| A. | 1m/s2 | B. | 2m/s2 | C. | 3m/s2 | D. | 4m/s2 |
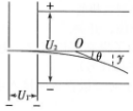 如图所示,一价氢离子和二价氦离子(不考虑二者间的相互作用),从静止开始经过同一电场加速,垂直打入偏转电场中,则它们( )
如图所示,一价氢离子和二价氦离子(不考虑二者间的相互作用),从静止开始经过同一电场加速,垂直打入偏转电场中,则它们( )| A. | 先后离开偏转电场,但出射点的位置不同 | |
| B. | 先后离开偏转电场,但出射点的位置相同 | |
| C. | 同时离开偏转电场,但出射点的位置不同 | |
| D. | 同时离开偏转电场,出射点的位置相同 |
| A. | 重力对三个物体做功的平均功率有可能相同 | |
| B. | 落地时,三个物体的重力的瞬时功率有可能相同 | |
| C. | 重力对竖直上抛的物体做功最多,对竖直下抛的物体做功最少 | |
| D. | 三个物体落地时速率一定相同 |
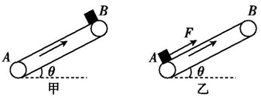 如图甲所示,倾斜传送带倾角θ=37°,两端AB间距离L=4m,传送带以4m/s的速度沿顺时针转动,一质量为1kg的小滑块从传送带顶端B点由静止释放下滑,到A时用时2s,g=10m/s2,sin 37°=0.6,cos 37°=0.8.
如图甲所示,倾斜传送带倾角θ=37°,两端AB间距离L=4m,传送带以4m/s的速度沿顺时针转动,一质量为1kg的小滑块从传送带顶端B点由静止释放下滑,到A时用时2s,g=10m/s2,sin 37°=0.6,cos 37°=0.8.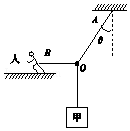 如图所示,质量m1=8kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上的质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,设最大静摩擦力等于滑动摩擦力) 求:
如图所示,质量m1=8kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上的质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,设最大静摩擦力等于滑动摩擦力) 求: