题目内容
5.如图甲所示,A、B为光滑水平地面上相距d的两挡板,在A、B的之间有一质量为m的质点P.若在P上加上如图乙所示随时间t变化的作用力F(取向右为F的正方向),在t=0时质点P位于A、B间的中点处且初速为0.已知质点P能在A、B之间以最大的幅度运动而不与两板相碰,且质点P开始从中点运动到最右边,以后每次从最左边到最右边或从最右边到最左边的过程中,力F只改变一次.要求: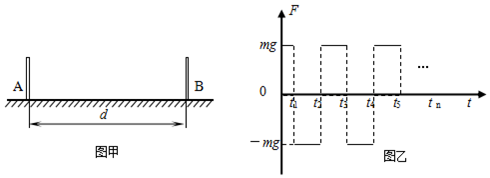
(1)求质点P由AB的中点从静止开始第一次运动到最右边的时间t;
(2)导出图乙中时刻t2的表达式;
(3)导出图乙中时刻tn的表达式.
分析 (1)质点从B板向A板先做加速运动,后做减速运动,位移之和等于$\frac{1}{2}$d,由速度公式和位移公式列式求解t的表达式.
(2)寻找每次加速和减速的规律,得出tn的表达式
解答 解:(1)质点运动加速度大小a=$\frac{F}{m}$=g
在t=0时,P自A、B间的中点向右作初速为0的匀加速运动,加速度为g.经过时间t1,P的速度变为v1,此时加速度变为向左,P向右作匀减速运动,再经过t1,P正好达到B板且速度变为0.故有
v1=g t1
0=v1-gt1
$\frac{1}{2}$d=$\frac{1}{2}$g${t}_{1}^{2}$+v1t1-$\frac{1}{2}$g${t}_{1}^{2}$由以上各式得t1=$\frac{\sqrt{2}}{2}\sqrt{\frac{d}{g}}$得t=t1+t1=$\sqrt{2}\sqrt{\frac{d}{g}}$
(2)P由B板处向左做匀加速运动,经过时间t2,P的速度变为v2,方向向左.此时加速度变为向右,P向左作匀减速运动,再经过t3,P正好达到A板且速度变为0.故有
v2=gt2
0=v2-gt3
d=$\frac{1}{2}$g${t}_{2}^{2}$+v2t3-$\frac{1}{2}$g${t}_{3}^{2}$由以上各式得 t2=t3=$\sqrt{\frac{d}{g}}$则 t2=t1+t1+t2=($\sqrt{2}$+1)$\sqrt{\frac{d}{g}}$质点P又由A板向右作匀加速运动,经过时间t4,速度变为v3,此时加速度变为向左,P向右作匀减速运动,经过t5,P正好达到B板且速度变为0.故有
v3=gt4
0=v3-gt5
d=$\frac{1}{2}$g${t}_{4}^{2}$+v3t5-$\frac{1}{2}$g${t}_{5}^{2}$由上得 t4=t5=$\sqrt{\frac{d}{g}}$t3=t2+t3+t4=( $\sqrt{2}$+3)$\sqrt{\frac{d}{g}}$根据上面分析,除第一次P从中点运动到最右点外,以后每次从从最左边到最右边或从最右边到最左边的运动,都是先做匀加速运动,再做匀减速运动,且每次匀加速运动和匀减速运动的时间相等,即
t2=t3=t4=t5=…=$\sqrt{\frac{d}{g}}$则tn=t+(2n-3)t2 (n≥2)
得tn=( $\sqrt{2}$+2n-3)$\sqrt{\frac{d}{g}}$(n≥2)
答:(1)质点P从AB的中点从静止开始出发第一次运动到最右点的时间t为 $\sqrt{2}\sqrt{\frac{d}{g}}$;
(2)导出图乙中时刻t2的表达式为t2=$\sqrt{\frac{d}{g}}$;
(3)导出图乙中时刻tn的表达式为tn=( $\sqrt{2}$+2n-3)$\sqrt{\frac{d}{g}}$(n≥2)
点评 本题是质点在周期性变化的作用力作用下的运动问题,分析质点的运动情况、把握运动规律是关键


| A. | 当火车的速率小于v时,火车将有向外侧冲出轨道的危险 | |
| B. | 当火车速率小于v时,外轨将受到轮缘的挤压 | |
| C. | 当火车的速率大于v时,外轨将受到轮缘的挤压 | |
| D. | 当火车的质量改变时,规定的行驶速度也改变 |
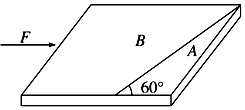 将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对放在一起,现用水平力F推B物体,使A、B整体保持矩形沿F方向匀速运动,则( )
将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并对放在一起,现用水平力F推B物体,使A、B整体保持矩形沿F方向匀速运动,则( )| A. | 物体A在水平方向上受到三个力的作用,且合力为零 | |
| B. | 物体A在水平方向上受到两个力的作用,且合力为零 | |
| C. | B对A的作用力方向与F方向相同 | |
| D. | B对A的压力大于桌面对A的摩擦力 |
| A. | 用手捏面包,面包体积会缩小,说明分子之间有间隙 | |
| B. | 温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同 | |
| C. | 布朗运动不是液体分子的运动,但它能说明分子永不停息地做无规则运动 | |
| D. | 分子间的距离r存在某一值r0,当r大于r0时,分子间斥力大于引力;当r小于r0时分子间斥力小于引力 |
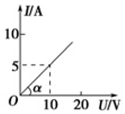
| A. | 通过电阻的电流与两端电压成正比 | |
| B. | 电阻R=0.5Ω | |
| C. | 因I-U图象的斜率表示电阻的倒数,故R=$\frac{1}{tanα}$=1.0Ω | |
| D. | 在R两端加上6.0V的电压时,每秒通过电阻横截面的电荷量是6.0C |
| A. | 电子秤中用到了力传感器 | |
| B. | 话筒是一种常见的声波传感器,其作用是将声信号转换为电信号 | |
| C. | 如图磁电式仪表的线圈常用铝框做骨架,把线圈绕在铝框上,如果将铝框换为同规格铁框不会影响仪表的精度 | |
| D. | 电感较大的电路,在开关断开时会产生电火花,烧蚀接触点,甚至引起人身伤害 |

| A. | 甲、乙两单摆的摆长不相等 | B. | 甲摆的振幅比乙摆大 | ||
| C. | 甲摆的机械能比乙摆大 | D. | 在t=0.5 s时乙摆摆线张力最大 |
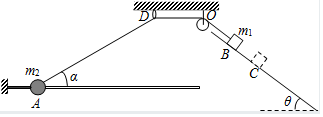 如图所示,一根不可伸长的轻细绳穿过光滑小环D,绕过轻质光滑定滑轮O,一端与物块m1连接,另一端与穿在光滑水平细杆上的小球m2连接,m2左端通过水平细线固定在竖直墙壁上,整个装置在同一竖直平面内.当m2静止在A点时,轻细绳与水平面的夹角为α=30°,D、A间的距离为1.2m.已知斜面倾角θ=37°,m1=2kg,m2=1kg,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,细杆、斜面足够长.求:
如图所示,一根不可伸长的轻细绳穿过光滑小环D,绕过轻质光滑定滑轮O,一端与物块m1连接,另一端与穿在光滑水平细杆上的小球m2连接,m2左端通过水平细线固定在竖直墙壁上,整个装置在同一竖直平面内.当m2静止在A点时,轻细绳与水平面的夹角为α=30°,D、A间的距离为1.2m.已知斜面倾角θ=37°,m1=2kg,m2=1kg,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,细杆、斜面足够长.求: