题目内容
一个半径是地球3倍、质量是地球36倍的行星,它表面的重力加速度是地球表面重力加速度的( )
| A.4倍 | B.6倍 | C.13.5倍 | D.18倍 |
A
解析试题分析:根据万有引力定律和牛顿第二定律可得: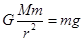 ,故有重力加速度
,故有重力加速度 ,所以可求得行星表面的重力加速度与地球重力加速度之比为
,所以可求得行星表面的重力加速度与地球重力加速度之比为 ,故只有A正确。
,故只有A正确。
考点:万有引力定律

我国“二炮”的一系列导弹,在“北斗”定位系统的引导下,能实现精确打击移动目标和固定目标。假设从地面上A点发射一枚远程弹道导弹,仅在地球引力作用下,沿ACB椭圆轨道飞行击中地面目标B, C为轨道的远地点,距地面高度为h,若ACB轨迹长恰好为整个椭圆的一半。已知地球半径为R,地球质量为M,引力常量为G。则下列结论正确的是 ( )
A.导弹在C点的速度大于  |
| B.地球的球心位于导弹椭圆轨道的一个焦点上 |
C.导弹在C点的加速度等于 |
| D.导弹从A点到B点的飞行时间等于导弹飞行周期的一半 |
比较距地高度为21500km的地球中轨道卫星甲和距地高度为36000km的地球同步轨道卫星乙,下列说法正确的是
| A.卫星甲运行周期较大 |
| B.卫星乙运行的角速度较大 |
| C.甲、乙卫星受到地球的引力大小可能相同 |
| D.卫星乙的向心加速度与静止在地球赤道上物体的向心加速度大小相同 |
甲、乙为两颗地球卫星,其中甲为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨道均可视为圆轨道.以下判断正确的是
| A.甲的周期大于乙的周期 |
| B.乙的速度大于第一宇宙速度 |
| C.甲的加速度小于乙的加速度 |
| D.甲在运行时能经过北极的正上方 |
甲、乙为两颗地球卫星,其中甲为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨道均可视为圆轨道。以下判断正确的是( )
| A.甲的周期小于乙的周期 |
| B.乙的速度大于第一宇宙速度 |
| C.甲的加速度小于乙的加速度 |
| D.甲在运行时能经过北极的正上方 |
2012年6月18日,我国“神舟九号”与“天宫一号”成功实现交会对接,如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟九号”运行轨道,在实现交会对接前,“神舟九号”要进行多次变轨,则( )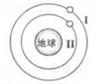
| A.“神舟九号”在圆形轨道Ⅱ的运行速率大于7.9 km/s |
| B.“天宫一号”的运行速率小于“神舟九号”在轨道Ⅱ上的运行速率 |
| C.“神舟九号”变轨前后机械能守恒 |
| D.“天宫一号”的向心加速度大于“神舟九号” 在轨道Ⅱ上的向心加速度 |
为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,科学家可以控制卫星上的电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2,地球半径R=6400km,地球自转周期为24h。某宇航员在地球表面测得体重为800N,他随升降机垂直地面上升,某时刻升降机加速度为10m/s2,方向竖直向上,这时此人再次测得体重为850N,忽略地球公转的影响,根据以上数据( )
| A.可以求出升降机此时所受万有引力的大小 |
| B.可以求出此时宇航员的动能 |
| C.可以求出升降机此时距地面的高度 |
| D.如果把绳的一端搁置在同步卫星上,可知绳的长度至少有多长 |
2012年6月18日,“神舟九号”飞船与“天宫一号”目标飞行器成功实现自动交会对接。设地球半径为R,地面重力加速度为g。对接成功后“神州九号”和“天宫一号”一起绕地球运行的轨道可视为圆轨道,轨道离地面高度约为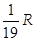 ,运行周期为T,引力常量为G,则
,运行周期为T,引力常量为G,则
| A.对接成功后,“神舟九号”飞船里的宇航员受到的重力为零 |
B.对接成功后,“神舟九号”飞船的加速度为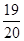 g g |
C.对接成功后,“神舟九号”飞船的线速度为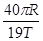 |
D.地球质量为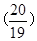 3 3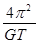 R2 R2 |
对于万有引力定律的表达式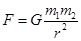 ,下面说法中正确的是( )
,下面说法中正确的是( )
| A.当r趋近于零时,万有引力趋于无穷大 |
| B.公式中G为引力常量,它是由实验测得的,而不是人为规定的 |
| C.若m1>m2,则m1受到的引力大于m2受到的引力 |
| D.m1与m2受到的引力大小相等,是一对平衡力 |