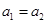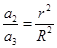题目内容
为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,科学家可以控制卫星上的电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2,地球半径R=6400km,地球自转周期为24h。某宇航员在地球表面测得体重为800N,他随升降机垂直地面上升,某时刻升降机加速度为10m/s2,方向竖直向上,这时此人再次测得体重为850N,忽略地球公转的影响,根据以上数据( )
| A.可以求出升降机此时所受万有引力的大小 |
| B.可以求出此时宇航员的动能 |
| C.可以求出升降机此时距地面的高度 |
| D.如果把绳的一端搁置在同步卫星上,可知绳的长度至少有多长 |
CD
解析试题分析:根据牛顿第二定律:N-mg′=ma,可求出此时的重力加速度g′,升降机此时所受到的万有引力为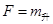 g′,因为不知道升降机的质量,所以求不出升降机所受的万有引力,故A错误;根据地球表面人的体重和地球表面的重力加速度,可知宇航员质量为80kg,但宇航员此时的速度无法求出,故选项B错误;再根据万有引力等于重力可得:
g′,因为不知道升降机的质量,所以求不出升降机所受的万有引力,故A错误;根据地球表面人的体重和地球表面的重力加速度,可知宇航员质量为80kg,但宇航员此时的速度无法求出,故选项B错误;再根据万有引力等于重力可得: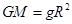 ,G
,G =mg′,可求出升降机此时距地面的高度h,故C正确;根据万有引力提供向心力可得:G
=mg′,可求出升降机此时距地面的高度h,故C正确;根据万有引力提供向心力可得:G =m(R+h)
=m(R+h)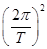 ,GM=gR2,T=24h,可求出同步卫星离地面的高度,此高度即为绳长的最小值,故D正确.故本题选CD.
,GM=gR2,T=24h,可求出同步卫星离地面的高度,此高度即为绳长的最小值,故D正确.故本题选CD.
考点:万有引力定律及其应用,卫星的速度、加速度、周期和轨道半径的关系

在讨论地球潮汐成因时,地球绕太阳运行轨道与月球绕地球运行轨道可视为圆周轨道.已知太阳质量约为月球质量的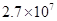 倍,地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍。关于太阳和月球对地球上相同质量海水的引力,以下说法正确的是
倍,地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍。关于太阳和月球对地球上相同质量海水的引力,以下说法正确的是
| A.太阳引力远小于月球引力 |
| B.太阳引力与月球引力相差不大 |
| C.月球对不同区域海水的吸引力大小有差异 |
| D.月球对不同区域海水的吸引力大小相等 |
一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为v,假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体的重力,物体静止时,弹簧测力计的示数为N,己知引力常量为G,则这颗行星的质量为( )
A.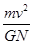 | B.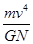 | C.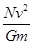 | D.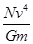 |
一个半径是地球3倍、质量是地球36倍的行星,它表面的重力加速度是地球表面重力加速度的( )
| A.4倍 | B.6倍 | C.13.5倍 | D.18倍 |
如图所示,将卫星发射至近地圆轨道1,然后再次点火,将卫星送入同步轨道3,轨道1、2相切于Q,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是 ( )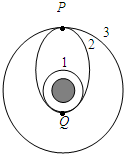
| A.卫星在轨道2上经过Q点时的速度小于它在轨道2上经过P点时的速度 |
| B.卫星在轨道1上经过Q点时的加速度等于它在轨道2上经过Q点时的加速度 |
| C.卫星在轨道1上的向心加速度小于它在轨道3上的向心加速度 |
| D.卫星在轨道3上的角速度小于在轨道1上的角速度 |
据媒体报道,天宫一号工作轨道为圆轨道,轨道高度约340km,运行周期127分钟。若还知道引力常量G和地球平均半径R,仅利用以上条件能求出的物理量是( )
| A.地球表面的重力加速度 |
| B.地球对卫星的吸引力 |
| C.卫星绕地运行的速度 |
| D.卫星绕地运行的加速度 |
随着世界航空事业的发展,深太空探测已逐渐成为各国关注的热点。假设深太空中有一颗外星球,质量是地球质量的2倍,半径是地球半径的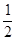 ,则下列判断正确的是( )
,则下列判断正确的是( )
| A.该外星球的同步卫星周期一定小于地球同步卫星周期 |
| B.某物体在该外星球表面上所受重力是它在地球表面上所受重力的8倍 |
| C.该外星球上第一宇宙速度是地球上第一宇宙速度的2倍 |
| D.绕该外星球的人造卫星和以相同轨道半径绕地球的人造卫星运行速度相同 |
如图,在火星与木星轨道之间有一小行星带.假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是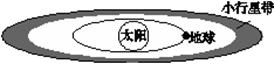
| A.太阳对各小行星的引力相同 |
| B.各小行星绕太阳运动的周期均小于一年 |
| C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值 |
| D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值 |
 ,速率为
,速率为 ;近地卫星的加速度大小为
;近地卫星的加速度大小为 ,运行速率为
,运行速率为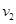 ;地球同步卫星的轨道半径为r ,加速度大小为
;地球同步卫星的轨道半径为r ,加速度大小为 ,运行速率为
,运行速率为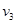 。则
。则