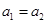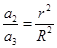题目内容
2012年6月18日,我国“神舟九号”与“天宫一号”成功实现交会对接,如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟九号”运行轨道,在实现交会对接前,“神舟九号”要进行多次变轨,则( )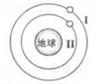
| A.“神舟九号”在圆形轨道Ⅱ的运行速率大于7.9 km/s |
| B.“天宫一号”的运行速率小于“神舟九号”在轨道Ⅱ上的运行速率 |
| C.“神舟九号”变轨前后机械能守恒 |
| D.“天宫一号”的向心加速度大于“神舟九号” 在轨道Ⅱ上的向心加速度 |
B
解析试题分析:第一宇宙速度7.9 km/s是卫星绕地球做圆周运动的最大环绕速度,则“神舟九号”在圆形轨道上的运行速率一定小于7.9km/s,A错误;根据万有引力提供向心力G =m
=m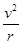 ,得v=
,得v= ,由题图可知天宫一号的轨道半径大于神舟九号的轨道半径,所以“天宫一号”的运行速率小于“神舟九号”在轨道Ⅱ上的运行速率,故B正确;神舟九号和天宫一号在各自的轨道上运动时机械能守恒,为实现两者对接,神舟九号需点火加速,做离心运动而实现变轨与天宫一号对接,点火加速后,机械能增加,故C错误;根据万有引力提供向心力G
,由题图可知天宫一号的轨道半径大于神舟九号的轨道半径,所以“天宫一号”的运行速率小于“神舟九号”在轨道Ⅱ上的运行速率,故B正确;神舟九号和天宫一号在各自的轨道上运动时机械能守恒,为实现两者对接,神舟九号需点火加速,做离心运动而实现变轨与天宫一号对接,点火加速后,机械能增加,故C错误;根据万有引力提供向心力G =ma,得a=
=ma,得a= ,可知天宫一号的轨道半径大于神舟八号的轨道半径,所以天宫一号”的向心加速度小于“神舟九号”在轨道Ⅱ上的向心加速度,故D错误.
,可知天宫一号的轨道半径大于神舟八号的轨道半径,所以天宫一号”的向心加速度小于“神舟九号”在轨道Ⅱ上的向心加速度,故D错误.
考点:万有引力定律及其应用,人造卫星的加速度、运行速率和轨道的关系

 阅读快车系列答案
阅读快车系列答案假设两颗“近地”卫星1和2的质量相同,都绕地球做匀速圆周运动,如图所示,卫星2的轨道半径更大些。两颗卫星相比较,下列说法中正确的是
| A.卫星1的向心加速度较小 |
| B.卫星1的动能较小 |
| C.卫星1的周期较小 |
| D.卫星1的机械能较小 |
“嫦娥三号”探测器计划于2013年底发射并在月球表面软着陆,目前选择在月球的虹湾地区着陆。作为先导星,“嫦娥二号”的主要任务是成功传回虹湾地区高分辨率图像,保证“嫦娥三号”探测器未来能够安全着陆。设想“嫦娥三号”贴近月球表面做匀速圆周运动,其周期为T。“嫦娥三号”在月球上着陆后,自动机器人用测力计测得质量为m的仪器重力为P。已知引力常量为G,由以上数据可以求出的物理量有( )
| A.月球的半径 |
| B.月球的质量 |
| C.月球表面的重力加速度 |
| D.月球绕地球做匀速圆周运动的向心加速度 |
一个半径是地球3倍、质量是地球36倍的行星,它表面的重力加速度是地球表面重力加速度的( )
| A.4倍 | B.6倍 | C.13.5倍 | D.18倍 |
引力常量G=6.67×10-11N·m2/kg2,太阳光传到地球约需8分钟,试估算太阳与地球质量之和的数量级为
| A.1024kg | B.1027kg | C.1030kg | D.1035kg |
将冥王星和土星绕太阳的运动都看做匀速圆周运动。已知冥王星绕太阳的公转周期约是土星绕太阳公转周期的8倍。那么冥王星和土星绕太阳运行的轨道半径之比约为
| A.2∶1 | B.4∶1 | C.8∶1 | D.16∶1 |
关于环绕地球运动的卫星,下列说法正确的是
| A.分别沿圆轨道和椭圆轨道运行的两颗卫星,不可能具有相同的周期 |
| B.沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率 |
| C.在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能不同 |
| D.沿不同轨道经过北京上空的两颗卫星,它们的轨道平面一定会重合 |
 ,加速度为
,加速度为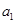 ,运行速率为
,运行速率为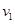 ;地球赤道上物体随地球自转的向心加速度为
;地球赤道上物体随地球自转的向心加速度为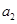 ,运行速率为
,运行速率为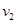 ,地球半径为
,地球半径为 。则
。则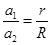
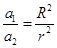
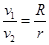
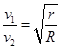
 ,速率为
,速率为 ;近地卫星的加速度大小为
;近地卫星的加速度大小为 ,运行速率为
,运行速率为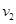 ;地球同步卫星的轨道半径为r ,加速度大小为
;地球同步卫星的轨道半径为r ,加速度大小为 ,运行速率为
,运行速率为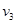 。则
。则