题目内容
13.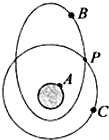 如图,A为置于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )
如图,A为置于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )| A. | 卫星C的运行速度大于物体A的速度 | |
| B. | 卫星B在P点的加速度大小与卫星C在该点加速度大小相等 | |
| C. | 卫星B运动轨迹的半长轴大于卫星C运动轨迹的半径 | |
| D. | 物体A和卫星C具有相同大小的加速度 |
分析 根据A、C的周期相等,知角速度相等,通过v=rω比较A、C速度的大小.因为卫星的周期一定,根据万有引力提供向心力确定其轨道半径一定.根据卫星所受的万有引力,通过牛顿第二定律比较加速度的大小.
解答 解:由题意可知,A、B、C绕地心运动的周期T相同,由ω=$\frac{2π}{T}$可知,A、B、C的角速度相等;
A、卫星C做圆周运动的半径大于A的半径,由v=ωr可知,C的线速度大于A的线速度,故A正确;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得,加速度:a=$\frac{GM}{{r}^{2}}$,在B点,G、M、r都相同,卫星B在P点的加速度大小与卫星C在该点加速度大小相等,故B正确;
C、由开普勒第三定律可知:$\frac{{r}_{B}^{3}}{{T}^{2}}$=$\frac{{r}_{C}^{3}}{{T}^{2}}$,则卫星B运动轨迹的半长轴与卫星C运动轨迹的半径相等,故C错误;
D、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得,加速度:a=$\frac{GM}{{r}^{2}}$,A、C的半径不同,它们的加速度不同,故D错误;
故选:AB
点评 解决本题的关键知道A和C的角速度相等,通过v=rω 比较线速度大小,注意物体A随地球做圆周运动不是靠万有引力提供向心力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.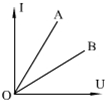 有A.B两个电阻,它们的伏安特性曲线如图所示,从图线可以判断 ( )
有A.B两个电阻,它们的伏安特性曲线如图所示,从图线可以判断 ( )
 有A.B两个电阻,它们的伏安特性曲线如图所示,从图线可以判断 ( )
有A.B两个电阻,它们的伏安特性曲线如图所示,从图线可以判断 ( )| A. | A的电阻值大于B的电阻值 | |
| B. | A的电阻值小于B的电阻值 | |
| C. | 两电阻串联时,电阻A消耗的功率较大 | |
| D. | 两电阻并联时,电阻B消耗的功率较大 |
18.以下的计时数据指时间的是( )
| A. | 某人用15s跑完100m | |
| B. | 早上6点起床 | |
| C. | 中央电视台新闻联播节目19时开播 | |
| D. | 天津开往德州的625次硬座普快列车于13h35min从天津西站发车 |
5.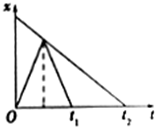 一条东西方向的平直公路边上有两块路牌A、B,A在西,B在东,一辆匀速行驶的汽车自东向西经过路牌B时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到汽车正上方立即折返,以原速率飞回A,过一段时间后,汽车也行驶到A.以向东为正方向,它们的位移一时间图象如图所示,图中t2=2t1,由图可知( )
一条东西方向的平直公路边上有两块路牌A、B,A在西,B在东,一辆匀速行驶的汽车自东向西经过路牌B时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到汽车正上方立即折返,以原速率飞回A,过一段时间后,汽车也行驶到A.以向东为正方向,它们的位移一时间图象如图所示,图中t2=2t1,由图可知( )
 一条东西方向的平直公路边上有两块路牌A、B,A在西,B在东,一辆匀速行驶的汽车自东向西经过路牌B时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到汽车正上方立即折返,以原速率飞回A,过一段时间后,汽车也行驶到A.以向东为正方向,它们的位移一时间图象如图所示,图中t2=2t1,由图可知( )
一条东西方向的平直公路边上有两块路牌A、B,A在西,B在东,一辆匀速行驶的汽车自东向西经过路牌B时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到汽车正上方立即折返,以原速率飞回A,过一段时间后,汽车也行驶到A.以向东为正方向,它们的位移一时间图象如图所示,图中t2=2t1,由图可知( )| A. | 小鸟的速率是汽车速率的三倍 | |
| B. | 相遇时小鸟与汽车位移的大小之比是3:1 | |
| C. | 小鸟飞行的总路程是汽车的1.5倍 | |
| D. | 小鸟和汽车在0~t2时间内位移相等 |
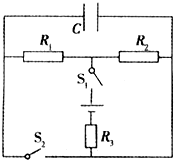 如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20 μF;已知电源电动势E=4V,内阻r=0.5Ω.求:
如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20 μF;已知电源电动势E=4V,内阻r=0.5Ω.求: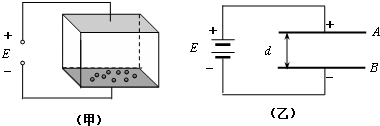
 在验证机械能守恒定律的实验中,质量为m=1.00kg的重物自由下落,在纸带上打出了一系列的点,如图所示,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,g取9.8m/s2.求:
在验证机械能守恒定律的实验中,质量为m=1.00kg的重物自由下落,在纸带上打出了一系列的点,如图所示,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,g取9.8m/s2.求: