14.若集合A={x|x=in,n∈N+}(i是虚数单位),B={1,-1},则A∩B等于( )
| A. | {-1} | B. | {1} | C. | ∅ | D. | {1,-1} |
13.已知p:?x∈R,x2-x+1>0,q:?x∈(0,+∞),sinx>1,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∨q | C. | p∨¬q | D. | ¬p∧¬q |
10.设函数g(x)=x2f(x),若函数f(x)为定义在R上的奇函数,其导函数为f′(x),对任意实数x满足x2f′(x)>2xf(-x),则不等式g(x)<g(1-3x)的解集是( )
| A. | $({\frac{1}{4},+∞})$ | B. | (0,$\frac{1}{4}$) | C. | $({-∞,\frac{1}{4}})$ | D. | $({-∞,\frac{1}{4}})∪({\frac{1}{4},+∞})$ |
9.函数y=1+logax(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中mn>0,则$\frac{1}{m}+\frac{3}{n}$的最小
值为( )
值为( )
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
8.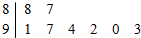 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
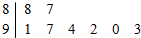 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
7.在复平面内复数$z=\frac{ai+1}{1-i}$对应的点在第一象限,则实数a的取值可以为( )
0 251702 251710 251716 251720 251726 251728 251732 251738 251740 251746 251752 251756 251758 251762 251768 251770 251776 251780 251782 251786 251788 251792 251794 251796 251797 251798 251800 251801 251802 251804 251806 251810 251812 251816 251818 251822 251828 251830 251836 251840 251842 251846 251852 251858 251860 251866 251870 251872 251878 251882 251888 251896 266669
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |