题目内容
10．设函数g（x）=x2f（x），若函数f（x）为定义在R上的奇函数，其导函数为f′（x），对任意实数x满足x2f′（x）＞2xf（-x），则不等式g（x）＜g（1-3x）的解集是（ ）| A． | $（{\frac{1}{4}，+∞}）$ | B． | （0，$\frac{1}{4}$） | C． | $（{-∞，\frac{1}{4}}）$ | D． | $（{-∞，\frac{1}{4}}）∪（{\frac{1}{4}，+∞}）$ |
分析 由题意和乘积的导数可得奇函数g（x）=x2f（x）在R上单调递增，可化原不等式为x＜1-3x，解之可得．
解答 解：由题意可得函数g（x）=x2f（x）为R上的奇函数，
∵x2f′（x）＞2xf（-x），∴x2f′（x）+2xf（x）＞0，
∴g′（x）=x2f（x）=2xf（x）+x2f′（x）＞0，
∴奇函数g（x）=x2f（x）在R上单调递增，
∴不等式g（x）＜g（1-3x）可化为x＜1-3x，
解得x＜$\frac{1}{4}$
故选：C
点评 本题考查函数的单调性和导数的关系，涉及函数的奇偶性，属基础题．
练习册系列答案
相关题目
20．
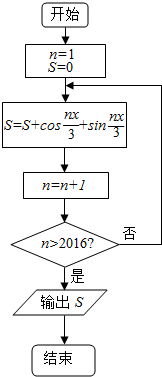如图所示程序框图中，输出S=（ ）
如图所示程序框图中，输出S=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | $\sqrt{3}$ |
15．设复数z=（x-1）+yi（x∈R，y≥0），若|z|≤1，则y≥x的概率为（ ）
| A． | $\frac{3}{4}+\frac{1}{2π}$ | B． | $\frac{1}{4}-\frac{1}{2π}$ | C． | $\frac{1}{2}-\frac{1}{π}$ | D． | $\frac{1}{2}+\frac{1}{π}$ |