题目内容
12.已知函数f(x)=mx2-x+lnx.(1)当m=-1时,求f(x)的极大值;
(2)若在函数f(x)的定义域内存在区间D,使得该函数在区间D上为减函数,求实数m的取值范围;
(3)当$0<m≤\frac{1}{2}$时,若曲线C:y=f(x)在点x=1处的切线l与曲线C有且只有一个公共点,求m的值或取值范围.
分析 (1)当m=-1时,求出函数的解析式,定义域,求出导函数,求出极值点,推出结果即可.
(2)(法一)$f'(x)=2mx-1+\frac{1}{x}=\frac{{2m{x^2}-x+1}}{x}$,通过当m≤0,当m>0时,求解实数m的取值范围.
(法二)$f'(x)=2mx-1+\frac{1}{x}=\frac{{2m{x^2}-x+1}}{x}$,问题成立只需m<u(x)max(x∈(0,+∞)),然后求解实数m的取值范围.
(3)求出切线方程,转化mx2-x+lnx=2mx-m-1在(0,+∞)上有且只有一解.构造函数g(x)=mx2-x+lnx-(2mx-m-1),求出函数g(x)有零点x=1.通过求解导函数,讨论当$m=\frac{1}{2}$时,当$0<m<\frac{1}{2}$时,判断函数的单调性,利用函数的零点.推出m的范围.
解答 解:(1)当m=-1时,f(x)=mx2-x+lnx=-x2-x+lnx,其定义域(0,+∞).
又$f'(x)=-2x-1+\frac{1}{x}=\frac{{-2{x^2}-x+1}}{x}=-\frac{x+1}{x}(\;2x-1\;)$.
∵$-\frac{x+1}{x}<0$,故由f′(x)=0,得$x=\frac{1}{2}$.…(1分)
∴当$0<x<\frac{1}{2}$时,f′(x)>0,f(x)递增;当$x>\frac{1}{2}$,f′(x)<0,f(x)递减.
因此当$x=\frac{1}{2}$时,f(x)取得极大值$f(\;\frac{1}{2}\;)=-\frac{3}{4}-ln2$;…(2分)
(2)(法一)$f'(x)=2mx-1+\frac{1}{x}=\frac{{2m{x^2}-x+1}}{x}$,即2mx2-x+1<0在(0,+∞)上有解.
当m≤0显然成立; …(4分)
当m>0时,由于函数y=2mx2-x+1的图象的对称轴$x=\frac{1}{4m}>0$,故须且
只须△>0,即1-8m>0,故$m<\frac{1}{8}$.…(5分)
综上所述得$m<\frac{1}{8}$,故实数m的取值范围为$(\;-∞\;,\;\frac{1}{8}\;)$;…(6分)
(若f'(x)≤0在(0,+∞)上有解,最后有检验也是可以的)
(法二)$f'(x)=2mx-1+\frac{1}{x}=\frac{{2m{x^2}-x+1}}{x}$,即2mx2-x+1<0在(0,+∞)上有解.
即2mx2-x+1<0在(0,+∞)能成立,
即$m<\frac{x-1}{{2{x^2}}}$,设$u(x)=\frac{x-1}{{2{x^2}}}$,问题成立只需m<u(x)max(x∈(0,+∞))…(5分)
∵$u(x)=-\frac{1}{2}({\frac{1}{x}-\frac{1}{2}})+\frac{1}{8}≤\frac{1}{8}$,
∴$m<\frac{1}{8}$故实数m的取值范围为$(\;-∞\;,\;\frac{1}{8}\;)$;…(6分)
(3)因为f(1)=m,f′(1)=2m,故切线方程为y-m+1=2m(x-1),即y=2mx-m-1,…(7分)
从而方程mx2-x+lnx=2mx-m-1在(0,+∞)上有且只有一解.
设g(x)=mx2-x+lnx-(2mx-m-1),则g(x)在(0,+∞)上
有且只有一个零点,又g(1)=0,故函数g(x)有零点x=1.…(8分)
则$g'(x)=2mx-1+\frac{1}{x}-\;2m=\frac{{2m{x^2}-(\;2m+1\;)x+1}}{x}=\frac{(\;2mx-1\;)(\;x-1\;)}{x}$.
当$m=\frac{1}{2}$时,g′(x)≥0,又g(x)不是常数函数,故g(x)在(0,+∞)上递增.
∴函数g(x)有且只有一个零点x=1,满足题意;…(9分)
当$0<m<\frac{1}{2}$时,由g′(x)=0,得$x=\frac{1}{2m}$,或x=1.且$\frac{1}{2m}>1$
由g′(x)>0,得0<x<1,或$x>\frac{1}{2m}$;由g′(x)<0,得$1<x<\frac{1}{2m}$;
故当x在(0,+∞)上变化时,g′(x)、g(x)的变化情况如下表:(此表可省略)
| x | (0,1) | 1 | $(\;1\;,\;\frac{1}{2m}\;)$ | $\frac{1}{2m}$ | $(\;\frac{1}{2m}\;,\;+∞\;)$ |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
又$g(x)=mx[x-(\;2+\frac{1}{m}\;)]+m+lnx+1$.∴$g(\;2+\frac{1}{m}\;)>0$,
故在$(\;\frac{1}{2m}\;,\;+∞\;)$上,函数g(x)又有一个零点,不符;…(11分)
综上所述得$m=\frac{1}{2}$.…(12分)
点评 本题考查函数的对数的应用,函数的极值点以及单调性,考查分类讨论思想以及转化思想的应用,考查分析问题解决问题的能力.

| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
| A. | 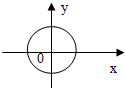 | B. | 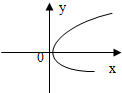 | C. |  | D. | 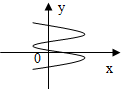 |