题目内容
5.把sin$\frac{π}{12}$,sin$\frac{5}{12}π$,cos$\frac{5}{7}π$,tan$\frac{5}{12}π$由小到大排列为$cos\frac{5π}{7}$<$sin\frac{π}{12}$<$sin\frac{5}{12}π$<$tan\frac{5}{12}π$.分析 作出单位圆、正弦线、余弦线、正切线,由此能比较sin$\frac{π}{12}$,sin$\frac{5}{12}π$,cos$\frac{5}{7}π$,tan$\frac{5}{12}π$的大小.
解答  解:作出单位圆,如图:
解:作出单位圆,如图:
∠M1OP1=$\frac{π}{12}$,∠M2OP2=$\frac{5π}{12}$,∠AOP3=$\frac{5π}{7}$,
∴sin$\frac{π}{12}$=M1P1,sin$\frac{5}{12}π$=M2P2,cos$\frac{5}{7}π$=OM3,tan$\frac{5}{12}π$=AT,
结合单位圆得到$cos\frac{5π}{7}$<$sin\frac{π}{12}$<$sin\frac{5}{12}π$<$tan\frac{5}{12}π$.
故答案为:$cos\frac{5π}{7}$<$sin\frac{π}{12}$<$sin\frac{5}{12}π$<$tan\frac{5}{12}π$.
点评 本题考查三角函数值大小的比较,是基础题,解题时要注意单位圆、正弦线、余弦线、正切线的性质的合理运用.

练习册系列答案
相关题目
10.设函数g(x)=x2f(x),若函数f(x)为定义在R上的奇函数,其导函数为f′(x),对任意实数x满足x2f′(x)>2xf(-x),则不等式g(x)<g(1-3x)的解集是( )
| A. | $({\frac{1}{4},+∞})$ | B. | (0,$\frac{1}{4}$) | C. | $({-∞,\frac{1}{4}})$ | D. | $({-∞,\frac{1}{4}})∪({\frac{1}{4},+∞})$ |
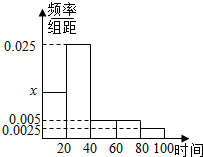 我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].